题目内容
5.若数列{an}满足a1=12,a1+2a2+3a3+…+nan=n2an,则a2017=$\frac{12}{2017}$.分析 通过a1+2a2+3a3+…+nan=n2an与当n≥2时a1+2a2+3a3+…+(n-1)an-1=(n-1)2an-1作差,进而可知nan=(n-1)an-1=…=2a2=a1,代入计算即得结论.
解答 解:因为a1+2a2+3a3+…+nan=n2an,
所以当n≥2时a1+2a2+3a3+…+(n-1)an-1=(n-1)2an-1,
两式相减得:nan=n2an-(n-1)2an-1,即n(n-1)an=(n-1)2an-1,
所以nan=(n-1)an-1=…=2a2=a1,
由a1=12可知an=$\frac{{a}_{1}}{n}$=$\frac{12}{n}$,
所以a2017=$\frac{12}{2017}$,
故答案为:$\frac{12}{2017}$.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
13.已知函数f(x)=ax-x2-lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
20.“a>1“是“$\frac{1}{a}$<1“的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
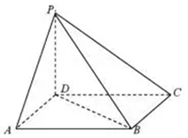 如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.