题目内容
1.已知点P在抛物线y=x2上,点Q在圆(x-4)2+(y+$\frac{1}{2}$)2=1上,则|PQ|的最小值为( )| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
分析 设P(t,t2),求出|PC|2=t4+2t2-8t+16+$\frac{1}{4}$,构造函数,利用函数的导数求解函数的最小值,由此能求出|PQ|的最小值.
解答 解:∵点P在抛物线y=x2上,∴设P(t,t2),
∵圆(x-4)2+(y+$\frac{1}{2}$)2=1的圆心C(4,-$\frac{1}{2}$),半径r=1,
∴|PC|2=(4-t)2+($-\frac{1}{2}$-t2)2=t4+2t2-8t+16+$\frac{1}{4}$,
令y=|PC|2=t4+2t2-8t+16+$\frac{1}{4}$,y′=4t3+4t-8=0,可得t3+t-2=0,解得t=1,当t<1时,y′<0,当t>1,y′>0,可知函数在t=1时取得最小值,|PC|2min=$\frac{45}{4}$
|PQ|的最小值=$\frac{3\sqrt{5}}{2}-1$.
故选:A.
点评 本题考查的知识要点:两点间的距离公式的应用,函数的导数的应用,考查圆的方程和抛物线方程的应用,及相关的运算问题.

练习册系列答案
相关题目
9.等差数列{an}的公差为2,若a2,a4,a8成等比数列,设Sn是数列{an}的前n项和,则S10的值为( )
| A. | 110 | B. | 90 | C. | 55 | D. | 45 |
13.已知函数f(x)=ax-x2-lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
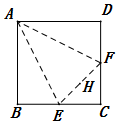 如图,在正方形ABCD中,E,F分别为BC,CD的中点,H为EF的中点,沿AE,EF,FA将正方形折起,使B,C,D重合于点O,构成四面体,则在四面体A-OEF中,下列说法不正确的序号是②.
如图,在正方形ABCD中,E,F分别为BC,CD的中点,H为EF的中点,沿AE,EF,FA将正方形折起,使B,C,D重合于点O,构成四面体,则在四面体A-OEF中,下列说法不正确的序号是②.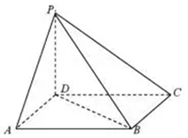 如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.