题目内容
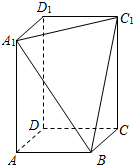 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.(Ⅰ)求棱AA1的长;
(Ⅱ)若A1C1的中点为O1,求异面直线BO1与A1D1所成角的余弦值.
考点:异面直线及其所成的角,棱柱的结构特征
专题:空间位置关系与距离,空间角
分析:(Ⅰ)设AA1=h,由题设VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1,可求出棱长.
(Ⅱ)因为在长方体中A1D1∥BC,所以∠O1BC即为异面直线BO1与A1D1所成的角(或其补角)那么借助于三角形求解得到结论.
(Ⅱ)因为在长方体中A1D1∥BC,所以∠O1BC即为异面直线BO1与A1D1所成的角(或其补角)那么借助于三角形求解得到结论.
解答:
解:(Ⅰ)设AA1=h,
由题设VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=10,
∴S正方形ABCD×h-
×S△A1B1C1×h=10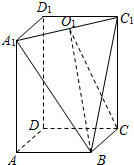
即2×2×h-
×
×2×2×h=10,解得h=3.
故A1A的长为3.
(Ⅱ)∵在长方体中,A1D1∥BC,
∴∠O1BC为异面直线BO1与A1D1所成的角(或其补角).
在△O1BC中,AB=BC=2,A1A=3,
∴AA1=BC1=
=
,A1O1=
A1C1=
,
∴O1B=O1C=
,
则cos∠O1BC=
=
=
.
∴异面直线BO1与A1D1所成角的余弦值为
.
由题设VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=10,
∴S正方形ABCD×h-
| 1 |
| 3 |

即2×2×h-
| 1 |
| 3 |
| 1 |
| 2 |
故A1A的长为3.
(Ⅱ)∵在长方体中,A1D1∥BC,
∴∠O1BC为异面直线BO1与A1D1所成的角(或其补角).
在△O1BC中,AB=BC=2,A1A=3,
∴AA1=BC1=
| 4+9 |
| 13 |
| 1 |
| 2 |
| 2 |
∴O1B=O1C=
| 11 |
则cos∠O1BC=
| BO12+BC2-O1C2 |
| 2•BO1•BC |
| 11+4-13 | ||
2×
|
| ||
| 22 |
∴异面直线BO1与A1D1所成角的余弦值为
| ||
| 22 |
点评:本题主要考查了点,线和面间的距离计算.解题的关键是利用了法向量的方法求点到面的距离.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
(
)2=( )
| 2i |
| 1-i |
| A、-2i | B、-4i |
| C、2i | D、4i |
设函数f(x)=x2+bx+c,且f(-1)=f(3),则( )
| A、f(-1)<c<f(1) |
| B、c<f(-1)<f(1) |
| C、f(1)<f(-1)<c |
| D、f(1)<c<f(-1) |
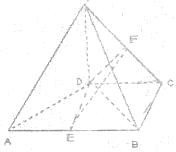 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.