题目内容
已知函数f(x)=ax-a•x,a≥e,e=2.71828…为自然对数的底数.
(Ⅰ)当a=e时,求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)设n∈N*,比较
lna与ln(a-1)+ln(2a-1)+ln(3a-1)+…+ln(na-1)的大小,并加以证明.
(Ⅰ)当a=e时,求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)设n∈N*,比较
| n(n+1) |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)当a=e时,求导数,确定切线的斜率,即可求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)
lna>ln(a-1)+ln(2a-1)+ln(3a-1)+…+ln(na-1),利用分析法进行证明,关键证明an>na-1.
(Ⅱ)
| n(n+1) |
| 2 |
解答:
解:(Ⅰ)∵a=e时,f(x)=ex-ex,
∴f′(x)=ex-e,
∴f′(1)=0,f(1)=0,
于是f(x)在点(1,f(1))处的切线方程为y=0.
(Ⅱ)
lna>ln(a-1)+ln(2a-1)+ln(3a-1)+…+ln(na-1),
理由如下:因为a≥e,
欲证
lna>ln(a-1)+ln(2a-1)+ln(3a-1)+…+ln(na-1)成立,
只需证a
>(a-1)(2a-1)(3a-1)…(na-1),
只需证an>na-1.
构造函数g(x)=
,则g′(x)=
.
因为a≥e,所以lna≥1.
令g′(x)>0,得x<
;g′(x)<0,得x>
.
所以函数g(x)在(-∞,
)单调递增;在(
,+∞)上单调递减.
所以函数g(x)的最大值为g(
)=
.所以
≤
,
所以
≤
,即ax-1≥e(x-1)lna,则
ax-ax+1=a[ax-1-(x-1)]+1-a≥a[e(x-1)lna-(x-1)]+1-a
>a[2(x-1)-(x-1)]+1-a=a(x-2)+1>0,
所以ax>ax-1.
取x=n,得an>na-1成立.
所以当a≥e时,
lna>ln(a-1)+ln(2a-1)+ln(3a-1)+…+ln(na-1)成立.
∴f′(x)=ex-e,
∴f′(1)=0,f(1)=0,
于是f(x)在点(1,f(1))处的切线方程为y=0.
(Ⅱ)
| n(n+1) |
| 2 |
理由如下:因为a≥e,
欲证
| n(n+1) |
| 2 |
只需证a
| n(n+1) |
| 2 |
只需证an>na-1.
构造函数g(x)=
| x |
| ax |
| 1-xlna |
| ax |
因为a≥e,所以lna≥1.
令g′(x)>0,得x<
| 1 |
| lna |
| 1 |
| lna |
所以函数g(x)在(-∞,
| 1 |
| lna |
| 1 |
| lna |
所以函数g(x)的最大值为g(
| 1 |
| lna |
| 1 |
| elna |
| x |
| ax |
| 1 |
| elna |
所以
| x-1 |
| ax-1 |
| 1 |
| elna |
ax-ax+1=a[ax-1-(x-1)]+1-a≥a[e(x-1)lna-(x-1)]+1-a
>a[2(x-1)-(x-1)]+1-a=a(x-2)+1>0,
所以ax>ax-1.
取x=n,得an>na-1成立.
所以当a≥e时,
| n(n+1) |
| 2 |
点评:本小题主要考查导数的几何意义、导数的应用(单调性、最值)、用点斜式求直线方程、比较不等式、证明不等式、数学归纳法等基础知识,考查推理论证能力、运算求解能力等,考查函数与方程思想、化归与转化思想、数形结合思想、有限与无限思想等.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
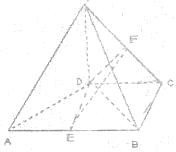 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则∠ACB=
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则∠ACB=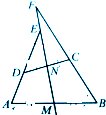 已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证:
已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证: