题目内容
 已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-7,其导函数y=f′(x)的图象经过点(-1,0),(2,0),如图所示,试求x0,a,b,c的值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-7,其导函数y=f′(x)的图象经过点(-1,0),(2,0),如图所示,试求x0,a,b,c的值.考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
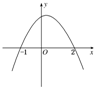
分析:由y=f′(x)的图象可知,在(-∞,-1)上f′(x)<0,在(-1,2)上f′(x)>0,在(2,+∞)上f′(x)<0,由此能求出x0,a,b,c的值.
解答:
 解:∵函数f(x)=ax3+bx2+cx,
解:∵函数f(x)=ax3+bx2+cx,
∴y′=3ax2+2bx+c,
由y=f′(x)的图象可知,
在(-∞,-1)上f′(x)<0,在(-1,2)上f′(x)>0,
在(2,+∞)上f′(x)<0,
故f(x)在(-∞,-1)上递减,在(-1,2)上递增,在(2,+∞)上递减.
因此,f(x)在x=-1处取得极小值,
所以x0=-1.
∵f(x)=ax3+bx2+cx,
∴f′(x)=3ax2+2bx+c.
故由f′(-1)=0,f′(2)=0,f(-1)=-7,
解得a=-2,b=3,c=12.
 解:∵函数f(x)=ax3+bx2+cx,
解:∵函数f(x)=ax3+bx2+cx,∴y′=3ax2+2bx+c,
由y=f′(x)的图象可知,
在(-∞,-1)上f′(x)<0,在(-1,2)上f′(x)>0,
在(2,+∞)上f′(x)<0,
故f(x)在(-∞,-1)上递减,在(-1,2)上递增,在(2,+∞)上递减.
因此,f(x)在x=-1处取得极小值,
所以x0=-1.
∵f(x)=ax3+bx2+cx,
∴f′(x)=3ax2+2bx+c.
故由f′(-1)=0,f′(2)=0,f(-1)=-7,
解得a=-2,b=3,c=12.
点评:本题考查x0,a,b,c的值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
 如图,椭圆C1:
如图,椭圆C1: 将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列:
将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列: