题目内容
 将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列:
将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
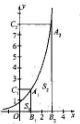
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如图,过A1,A2,…,An分别作x轴、y轴的垂线,与x轴、y轴分别相交于B1,B2,…,Bn;C1,C2,…,Cn,矩形OB1A1C1,OB2A2C2,…,OBnAnCn的分别面积为S1,S2,…,Sn,求S1+S2+…+Sn的值Tn.
考点:指数函数综合题
专题:函数的性质及应用
分析:(Ⅰ)正奇数组成的数列{an}的通项公式为an=2n-1,由题意可得,第五行的第一个数为a17=1+16×2=33,第五行到第十行的所有数共有24个,再利用等差数列的求和公式求得第五行到第十行的所有数的和.
(Ⅱ)由An(an,bn)在指数函数y=2x的图象上,可得 bn=2an=22n-1,求得 S1、S2、,…,Sn,可得Tn=1×2+3×23+5×25+…+(2n-1)•22n-1,再利用错位相减求得Tn的值.
(Ⅱ)由An(an,bn)在指数函数y=2x的图象上,可得 bn=2an=22n-1,求得 S1、S2、,…,Sn,可得Tn=1×2+3×23+5×25+…+(2n-1)•22n-1,再利用错位相减求得Tn的值.
解答:
解:(Ⅰ)正奇数组成的数列{an}是首项为2,且公差为2的等差数列,故有an=2n-1,
由题意可得,第五行的第一个数为a17=1+16×2=33,第五行到第十行的所有数共有24个,
故第五行到第十行的所有数的和为24×33+
×2=1344.
(Ⅱ)∵An(an,bn)在指数函数y=2x的图象上,∴bn=2an=22n-1,
∴S1=a1•b1=1×2=2,S2=a2•b2=3×8=24,…,Sn=an•bn=(2n-1)•22n-1.
∴Tn=1×2+3×23+5×25+…+(2n-1)•22n-1 ①,
∴4Tn=1×23+3×25+5×27+…+(2n-3)•22n-1+(2n-1)•22n+1 ②,
①-②可得-3Tn=2+2(23+25+27+…+22n-1)-(2n-1)22n+1=2(2+23+25+27+…+22n-1)-2-(2n-1)22n+1
=2×
-2-(2n-1)22n+1=(
-4n)•4n-
,
∴Tn=(
-
)•4n+
.
由题意可得,第五行的第一个数为a17=1+16×2=33,第五行到第十行的所有数共有24个,
故第五行到第十行的所有数的和为24×33+
| 24×23 |
| 2 |
(Ⅱ)∵An(an,bn)在指数函数y=2x的图象上,∴bn=2an=22n-1,
∴S1=a1•b1=1×2=2,S2=a2•b2=3×8=24,…,Sn=an•bn=(2n-1)•22n-1.
∴Tn=1×2+3×23+5×25+…+(2n-1)•22n-1 ①,
∴4Tn=1×23+3×25+5×27+…+(2n-3)•22n-1+(2n-1)•22n+1 ②,
①-②可得-3Tn=2+2(23+25+27+…+22n-1)-(2n-1)22n+1=2(2+23+25+27+…+22n-1)-2-(2n-1)22n+1
=2×
| 2×(1-4n) |
| 1-4 |
| 10 |
| 3 |
| 10 |
| 3 |
∴Tn=(
| 4n |
| 3 |
| 10 |
| 9 |
| 10 |
| 9 |
点评:本题主要考查等差数列的定义、性质、通项公式、前n项和公式的应用,指数函数的图象和性质应用,用错位相减法进行数列求和,属于中档题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-7,其导函数y=f′(x)的图象经过点(-1,0),(2,0),如图所示,试求x0,a,b,c的值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-7,其导函数y=f′(x)的图象经过点(-1,0),(2,0),如图所示,试求x0,a,b,c的值.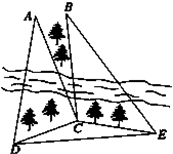 如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.
如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.