题目内容
设△ABC中的内角A、B、C所对的边长分别a、b、c,且cosB=
,b=2
(1)当a=
时,求角A的度数
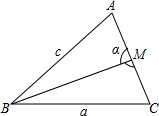
(2)设AC边的中线为BM,求BM长度的最大值.
| 4 |
| 5 |
(1)当a=
| 5 |
| 3 |
(2)设AC边的中线为BM,求BM长度的最大值.
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)由cosB的值,利用同角三角函数间的基本关系求出sinB的值,再由a,b的值,利用正弦定理求出sinA的值,即可确定出A的度数;
(2)设BM=m,∠AMB=α,在三角形ABM与三角形BCM中,分别利用余弦定理列出关系式,根据邻补角定义及诱导公式变形,消去α得到关系式,再利用余弦定理列出关系式,再利用基本不等式求出BM的最大值.
(2)设BM=m,∠AMB=α,在三角形ABM与三角形BCM中,分别利用余弦定理列出关系式,根据邻补角定义及诱导公式变形,消去α得到关系式,再利用余弦定理列出关系式,再利用基本不等式求出BM的最大值.
解答:
 解:(1)∵cosB=
解:(1)∵cosB=
>0,
∴sinB=
=
>
=sinA,
∵A<B,∴A=30°;
(2)设BM=m,∠AMB=α,
由余弦定理得:c2=m2+1-2m×cosα;a2=m2+1+mcosα,
整理得:2m2=a2+c2-2,
∵b2=a2+c2-2accosB,
∴a2+c2-
ac=4,即2ac=
(a2+c2-4),
∵2ac≤a2+c2,
∴
(a2+c2-4)≤a2+c2,
整理得:a2+c2≤20,即2m2=a2+c2-2≤18,
解得:0<m≤3,
则BM的最大值为3.
 解:(1)∵cosB=
解:(1)∵cosB=| 4 |
| 5 |
∴sinB=
| 1-cos2B |
| 3 |
| 5 |
| 1 |
| 2 |
∵A<B,∴A=30°;
(2)设BM=m,∠AMB=α,
由余弦定理得:c2=m2+1-2m×cosα;a2=m2+1+mcosα,
整理得:2m2=a2+c2-2,
∵b2=a2+c2-2accosB,
∴a2+c2-
| 8 |
| 5 |
| 5 |
| 4 |
∵2ac≤a2+c2,
∴
| 5 |
| 4 |
整理得:a2+c2≤20,即2m2=a2+c2-2≤18,
解得:0<m≤3,
则BM的最大值为3.
点评:此题考查了余弦定理,基本不等式的运用,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
将一颗骰子连续投掷两次,两次正面出现点数之和能被4整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
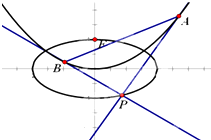 已知椭圆C1:
已知椭圆C1: