题目内容
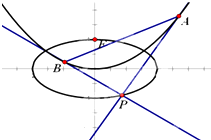 已知椭圆C1:
已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)若交点P在椭圆C1上,证明:点(k,m)在定圆上运动;并求S△ABP的最大时,直线AB的方程.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆C1的方程.
(Ⅱ)设A(x1,
),B(x2,
),利用导数据的几何意义分别求出切线PA方程:y=
x-
,切线PB方程:y=
x-
,联立方程组求出P点的坐标P(
,
),由
,消元得:x2-4kx-4m=0,由此利用韦达定理和点到直线AB的距离公能求出直线AB的方程.
|
(Ⅱ)设A(x1,
| ||
| 4 |
| ||
| 4 |
| x1 |
| 2 |
| x12 |
| 4 |
| x2 |
| 2 |
| x22 |
| 4 |
| x1+x2 |
| 2 |
| x1•x2 |
| 4 |
|
解答:
解:(Ⅰ)∵抛物线C2:x2=4y的焦点坐标F(0,1),
椭圆C1:
+
=1(a>b>0)的离心率
,
抛物线C2:x2=4y的焦点F恰好是椭圆短轴的一个端点,
∴
,解得:
,
∴椭圆C1的方程:
+y2=1.
(Ⅱ)设A(x1,
),B(x2,
),
由y=
,得y′=
,
∴切线PA方程:y=
x-
,
同理切线PB方程:y=
x-
,
联立方程
,
解得P点的坐标P(
,
),
又
,消元得:x2-4kx-4m=0,
由韦达定理得:
,
∴P点的坐标可化为P(2k,-m),而P点在椭圆上,∴k2+m2=1.
∴点(k,m)在单位圆上.
而|BC|=
|x1-x2|=
=
•
,
P点到直线AB的距离d=
,
S△ABP=
|BC|•d═4(k2+m)
=4(1-m2+m)
=4[-(m-
)2+
]
≤
,
即当m=
时取最大值.此时k=±
,
∴直线AB的方程为y=±
x+
.
椭圆C1:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
抛物线C2:x2=4y的焦点F恰好是椭圆短轴的一个端点,
∴
|
|
∴椭圆C1的方程:
| x2 |
| 4 |
(Ⅱ)设A(x1,
| ||
| 4 |
| ||
| 4 |
由y=
| x2 |
| 4 |
| x |
| 2 |
∴切线PA方程:y=
| x1 |
| 2 |
| x12 |
| 4 |
同理切线PB方程:y=
| x2 |
| 2 |
| x22 |
| 4 |
联立方程
|
解得P点的坐标P(
| x1+x2 |
| 2 |
| x1•x2 |
| 4 |
又
|
由韦达定理得:
|
∴P点的坐标可化为P(2k,-m),而P点在椭圆上,∴k2+m2=1.
∴点(k,m)在单位圆上.
而|BC|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| 16k2+16m |
P点到直线AB的距离d=
| |2k2+2m| | ||
|
S△ABP=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
5
| ||
| 2 |
即当m=
| 1 |
| 2 |
| ||
| 2 |
∴直线AB的方程为y=±
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
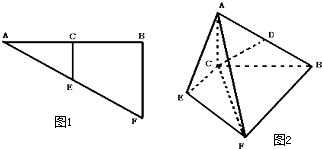 在Rt△ABF中,AB=2BF=4,C,E分别是AB,AF的中点(如图1).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如图2),已知D是AB的中点.
在Rt△ABF中,AB=2BF=4,C,E分别是AB,AF的中点(如图1).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如图2),已知D是AB的中点.
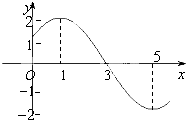 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<