题目内容
已知函数f（x）=x3+3x2-9x+1．
（1）求f（x）的极大值；
（2）若f（x）在[k，2]上的最大值为28，求k的取值范围．
（1）求f（x）的极大值；
（2）若f（x）在[k，2]上的最大值为28，求k的取值范围．
考点：利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题：导数的综合应用
分析：（1）由已知条件知f（x）的定义域为R，f'（x）=3x2+6x-9，令f'（x）=3x2+6x-9＞0，得x＞1或x＜-3，列表讨论能求出f（x）的极大值．
（2）由（1）知f（x）在[1，2]为增函数，在[-3，1]为减函数，（-∞，-3）为增函数，由此能求出k的取值范围．
（2）由（1）知f（x）在[1，2]为增函数，在[-3，1]为减函数，（-∞，-3）为增函数，由此能求出k的取值范围．
解答：
解：（1）∵f（x）=x3+3x2-9x+1，
∴f（x）的定义域为R，f'（x）=3x2+6x-9，
令f'（x）=3x2+6x-9＞0，得x＞1或x＜-3，
列表讨论：
∴当x=-3时，f（x）有极大值f（-3）=28．（5分）
（2）由（1）知f（x）在[1，2]为增函数，
在[-3，1]为减函数，（-∞，-3）为增函数，
且f（2）=3，f（-3）=28，（8分）
∵f（x）在[k，2]上的最大值为28，
∴所求k的取值范围为k≤-3，即k∈（-∞，-3]．（10分）
∴f（x）的定义域为R，f'（x）=3x2+6x-9，
令f'（x）=3x2+6x-9＞0，得x＞1或x＜-3，
列表讨论：
| x | （-∞，-3） | -3 | （-3，1） | 1 | （1，+∞） |
| f’（x） | + | 0 | - | 0 | + |
| f（x） | 单调递增↗ | 28 | 单调递减↘ | -4 | 单调递增↗ |
（2）由（1）知f（x）在[1，2]为增函数，
在[-3，1]为减函数，（-∞，-3）为增函数，
且f（2）=3，f（-3）=28，（8分）
∵f（x）在[k，2]上的最大值为28，
∴所求k的取值范围为k≤-3，即k∈（-∞，-3]．（10分）
点评：本题考查函数的极大值的求法，考查实数的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的灵活运用．
练习册系列答案
相关题目
已知f（x）=lnx+x-2，g（x）=xlnx+x-2在（1，+∞）上都有且只有一个零点，f（x）的零点为x1，g（x）的零点为x2，则（ ）
| A、1＜x2＜x1＜2 |
| B、1＜x1＜x2＜2 |
| C、1＜x1＜2＜x2 |
| D、2＜x2＜x1 |
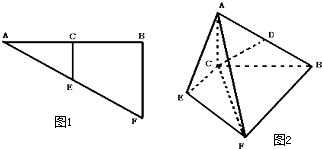在Rt△ABF中，AB=2BF=4，C，E分别是AB，AF的中点（如图1）．将此三角形沿CE对折，使平面AEC⊥平面BCEF（如图2），已知D是AB的中点．