题目内容
已知f(x)=cos2x+4sinx,求:
(1)f(-
)的值;
(2)f(x)的最大值以及取得最大值时x的值.
(1)f(-
| π |
| 4 |
(2)f(x)的最大值以及取得最大值时x的值.
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:展开二倍角的余弦,得到f(x)=-2sin2x+4sinx+1.
(1)直接取x=-
求f(-
)的值;
(2)利用配方法配方,求得f(x)的最大值并求得f(x)取得最大值时x的值.
(1)直接取x=-
| π |
| 4 |
| π |
| 4 |
(2)利用配方法配方,求得f(x)的最大值并求得f(x)取得最大值时x的值.
解答:
解:f(x)=cos2x+4sinx
=1-2sin2x+4sinx
=-2sin2x+4sinx+1.
(1)f(-
)=-2sin2(-
)+4sin(-
)+1
=-2×
-4×
+1=-2
;
(2)f(x)=-2sin2x+4sinx+1=-2(sinx-1)2+3.
当sinx=1,即x=
+2kπ,k∈Z时函数取得最大值3.
=1-2sin2x+4sinx
=-2sin2x+4sinx+1.
(1)f(-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=-2×
| 1 |
| 2 |
| ||
| 2 |
| 2 |
(2)f(x)=-2sin2x+4sinx+1=-2(sinx-1)2+3.
当sinx=1,即x=
| π |
| 2 |
点评:本题考查了三角函数中恒等变换应用,考查了配方法求函数的最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
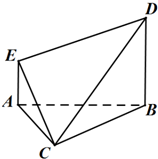 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.