题目内容
一次研究性课堂上,老师给出函数f(x)=
,甲、乙、丙三位同学在研究此函数的性质时分别给出下列命题:
甲:函数f(x)为偶函数;
乙:函数f(x)的值域为(-1,1);
丙:若x1≠x2则一定有f(x1)≠f(x2)
你认为上述三个命题中正确的个数有 个.
| x |
| 1+|x| |
甲:函数f(x)为偶函数;
乙:函数f(x)的值域为(-1,1);
丙:若x1≠x2则一定有f(x1)≠f(x2)
你认为上述三个命题中正确的个数有
考点:命题的真假判断与应用
专题:简易逻辑
分析:首先,求解函数的定义域,然后,借助于f(-x)和f(x)之间的关系,判断奇偶性;然后,借助于绝对值的几何意义,求解函数的值域问题;最后,借助于函数的单调性判断丙的说法正误.
解答:
解:∵函数f(x)的定义域为R,且f(-x)=
=-f(x),∴,函数f(x)为奇函数,所以,甲的说法是错误的;
f(x)=
,
当x≥0时,f(x)=
=
=1-
,
∴0≤f(x)<1,
当x<0时,f(x)=-
=-
=-1-
,
∴-1<f(x)<0,
函数f(x)的值域为(-1,1);所以,乙的说法正确;
对于丙的说法:函数在(0,+∞)上为增函数,证明如下:
取任意x1,x2∈(0,+∞),且x1<x2,
∵f(x1)-f(x2)=
-
=
∴x1<x2,∴f(x1)<f(x2),
∴函数在(0,+∞)上为增函数,
同理,可以证明函数在(-∞,0)上为增函数,
∴丙的说法是正确的,
∴正确的说法只有乙和丙,
故答案为2,
| -x |
| 1+|x| |
f(x)=
|
当x≥0时,f(x)=
| x |
| 1+x |
| x+1-1 |
| x+1 |
| 1 |
| 1+x |
∴0≤f(x)<1,
当x<0时,f(x)=-
| x |
| x-1 |
| x-1+1 |
| x-1 |
| 1 |
| x-1 |
∴-1<f(x)<0,
函数f(x)的值域为(-1,1);所以,乙的说法正确;
对于丙的说法:函数在(0,+∞)上为增函数,证明如下:
取任意x1,x2∈(0,+∞),且x1<x2,
∵f(x1)-f(x2)=
| 1 |
| 1+x2 |
| 1 |
| 1+x1 |
| x1-x2 |
| (1+x1)(1+x2) |
∴x1<x2,∴f(x1)<f(x2),
∴函数在(0,+∞)上为增函数,
同理,可以证明函数在(-∞,0)上为增函数,
∴丙的说法是正确的,
∴正确的说法只有乙和丙,
故答案为2,
点评:本题重点考查函数的基本性质,函数的定义域,奇偶性,单调性等知识,考查比较综合,属于中档题,难度中等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知集合A={x|x2-x<0},集合B={x|2x<4},则“x∈A”是“x∈B”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下面说法正确的是( )
| A、不存在既不是奇函数,有又不是偶函数的幂函数 |
| B、图象不经过点(-1,1)的幂函数一定不是偶函数 |
| C、如果两个幂函数的图象有三个公共点,那么这两个幂函数相同 |
| D、如果一个幂函数的图象不与y轴相交,则y=xα中α<0 |
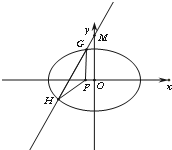 已知椭圆C:
已知椭圆C: