题目内容
7．已知△ABC为等边三角形，点M在△ABC外，且MB=2MC=2，则MA的最大值是3．分析 以BM为边作等边三角形BMK，推导出A在以K为圆心，以1为半径的圆上，由此能求出MA的最大值．
解答 
解：以BM为边作等边三角形BMK
则BM=BK=MK=2，
∵∠BMK=∠ABC=60°，
∴∠ABK=∠MBC，
又AB=BC，BK=BK，∴△ABK∽△CBM，
∴AK=MC=1，∴A在以K为圆心，以1为半径的圆上，
∴|MK|-1≤|AM|≤|MK|+1，
∴1≤|AM|≤3．
∴MA的最大值是3．
故答案为：3．
点评 本题考查线段长的最大值的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
相关题目
18．公差为1的等差数列{an}中，a1，a3，a6成等比数列，则{an}的前10项和为（ ）
| A． | 65 | B． | 80 | C． | 85 | D． | 170 |
15．已知三棱锥的三视图如图所示，则此三棱锥外接球的表面积为（ ）
| A． | 8$\sqrt{5}$π | B． | 8$\sqrt{6}$π | C． | 5π | D． | 6π |
2．下列函数中，既是奇函数又在区间（-1，1）上单调递减的函数是（ ）
| A． | f（x）=sinx | B． | f（x）=2cosx+1 | C． | f（x）=2x-1 | D． | $f（x）=ln\frac{1-x}{1+x}$ |
12．（1-x）6（1+x）4的展开式中x2的系数是（ ）
| A． | -4 | B． | -3 | C． | 3 | D． | 4 |
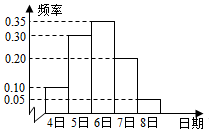北京铁路局针对今年春运客流量进行数据整理，调查北京西站从2月4日到2月8日的客流量，根据所得数据画出了五天中每日客流量的频率分布图，为了更详细地分析不同时间的客流人群，按日期用分层抽样的方法抽样，若从2月7日这个日期抽取了40人，则一共抽取的人数为200．