题目内容
11.已知数列{an}的前n项和为Sn,且${a_1}=1,{a_n}=\frac{{2{S_n}^2}}{{2{S_n}-1}}({n≥2})$,则S2016=$\frac{1}{4031}$.分析 ${a_1}=1,{a_n}=\frac{{2{S_n}^2}}{{2{S_n}-1}}({n≥2})$,可得(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,利用等差数列的通项公式即可得出.
解答 解:∵${a_1}=1,{a_n}=\frac{{2{S_n}^2}}{{2{S_n}-1}}({n≥2})$,
∴(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,
化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,
∴数列$\{\frac{1}{{S}_{n}}\}$是等差数列,首项为1,公差为2.
∴$\frac{1}{{S}_{n}}$=1+2(n-1)=2n-1.
∴Sn=$\frac{1}{2n-1}$.
则S2016=$\frac{1}{2×2016-1}$=$\frac{1}{4031}$.
故答案为:$\frac{1}{4031}$.
点评 本题考查了递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,F1,F2是椭圆的两个焦点,A为椭圆的右顶点,B为椭圆的上顶点.若在线段AB(不含端点)上存在不同的两个点A1,A2,使得△F1A1F2和△F1A2F2均为以F1F2为斜边的直角三角形,则椭圆的离心率的取值范围为( )
| A. | ($\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{5}-1}{2}$,1) | C. | (0,$\frac{\sqrt{5}-1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,1) |
2.下列函数中,既是奇函数又在区间(-1,1)上单调递减的函数是( )
| A. | f(x)=sinx | B. | f(x)=2cosx+1 | C. | f(x)=2x-1 | D. | $f(x)=ln\frac{1-x}{1+x}$ |
20.一个几何体的三视图如图所示,则该几何体的表面积等于( )


| A. | 5π | B. | 9π | C. | 16π | D. | 25π |
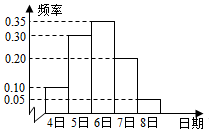 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.