题目内容
4.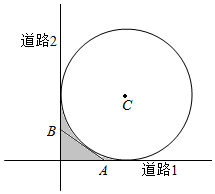 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
分析 分别由两条道路所在直线建立直角坐标系xOy.设A(a,0),B(0,b)(0<a<1,0<b<1),求得直线AB的方程和圆的方程,运用直线和圆相切的条件:d=r,求得a,b的关系,再由两点的距离公式和基本不等式,解不等式可得AB的最小值,及此时A,B的位置.
解答 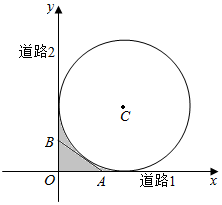 解:如图,分别由两条道路所在直线建立直角坐标系xOy.
解:如图,分别由两条道路所在直线建立直角坐标系xOy.
设A(a,0),B(0,b)(0<a<1,0<b<1),
则直线AB方程为$\frac{x}{a}$+$\frac{y}{b}$=1,即bx+ay-ab=0.
因为AB与圆C:(x-1)2+(y-1)2=1相切,所以$\frac{|b+a-ab|}{\sqrt{{b}^{2}+{a}^{2}}}$=1,
化简得ab-2(a+b)+2=0,即ab=2(a+b)-2,
因此AB=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{(a+b)^{2}-2ab}$=$\sqrt{(a+b)^{2}-4(a+b)+4}$
=$\sqrt{(a+b-2)^{2}}$,
因为0<a<1,0<b<1,所以0<a+b<2,
于是AB=2-(a+b).
又ab=2(a+b)-2≤($\frac{a+b}{2}$)2,
解得0<a+b≤4-2$\sqrt{2}$,或a+b≥4+2$\sqrt{2}$,
因为0<a+b<2,所以0<a+b≤4-2$\sqrt{2}$,
所以AB=2-(a+b)≥2-(4-2$\sqrt{2}$)=2$\sqrt{2}$-2,
当且仅当a=b=2-$\sqrt{2}$时取等号,
所以AB最小值为2$\sqrt{2}$-2,此时a=b=2-$\sqrt{2}$.
答:当A,B两点离道路的交点都为2-$\sqrt{2}$(百米)时,小道AB最短.
点评 本题考查基本不等式在最值问题中的运用,同时考查直线和圆相切的条件,考查化简整理的运算能力,属于中档题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
| A. | 8$\sqrt{5}$π | B. | 8$\sqrt{6}$π | C. | 5π | D. | 6π |
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
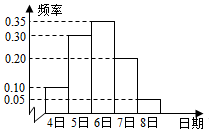 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.