题目内容
在半径为4的球面上有A、B、C三点(O为球心),已知AB=3,BC=5,AC=4,则点O的平面ABC的距离为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:由已知得BC为该三角形外接圆直径,其中点O'为其圆心,由球的特性可知OO'即为O到平面ABC的距离,由此能求出球心O到平面ABC的距离.
解答:
解:由已知,三角形ABC的外接圆圆心是BC的中点,
∵AB2+AC2=BC2,
∴△ABC为直角三角形,
∴BC为该三角形外接圆直径,其中点O'为其圆心,
由球的特性可知OO'即为O到平面ABC的距离,
∴OO'2=OB2-(
)2=16-
,
OO'=
,
∴球心O到平面ABC的距离为
.
故答案为:
.
∵AB2+AC2=BC2,
∴△ABC为直角三角形,
∴BC为该三角形外接圆直径,其中点O'为其圆心,
由球的特性可知OO'即为O到平面ABC的距离,
∴OO'2=OB2-(
| BC |
| 2 |
| 25 |
| 4 |
OO'=
| ||
| 2 |
∴球心O到平面ABC的距离为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
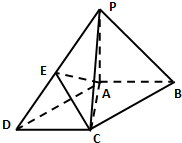 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
 某个容量1000的样本的频率分布直方图如图所示,则在区间[4,5]上的数据的频数为
某个容量1000的样本的频率分布直方图如图所示,则在区间[4,5]上的数据的频数为