题目内容
9.直线l的参数方程为$\left\{\begin{array}{l}x=2t-1\\ y=2t+1\end{array}\right.$(t为参数),圆C的圆心为C(0,1),且与x轴相切,若l与圆C交于A、B两点,则△ABC的面积为$\frac{1}{2}$.分析 求出直线l的直角坐标方程为x-y+2=0,圆C的直角坐标方程为x2+(y-1)2=1,联立直线与圆的方程,得A(0,2),B(-1,1),由此能求出△ABC的面积.
解答 解:∵直线l的参数方程为$\left\{\begin{array}{l}x=2t-1\\ y=2t+1\end{array}\right.$(t为参数),
∴直线l的直角坐标方程为x-y+2=0,
∵圆C的圆心为C(0,1),且与x轴相切,
∴圆C的直角坐标方程为x2+(y-1)2=1,
联立$\left\{\begin{array}{l}{x-y+2=0}\\{{x}^{2}+(y-1)^{2}=1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
∴A(0,2),B(-1,1),
∵C(0,1),∴BC=1,AC=1,AC⊥BC,
∴△ABC的面积S=$\frac{1}{2}×AC×BC$=$\frac{1}{2}×1×1=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查三角形面积的求法,是中档题,解题时要认真审题,注意圆与直线的位置关系、点到直线距离公式、极坐标与直角坐标互化公式等知识点的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.已知集合A={1,2,3},B={0,1,2},则A∩B的子集个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 16 |
17.将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D.则四面体ABCD的内切球的半径为( )
| A. | 1 | B. | $2\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{3}$ |
14.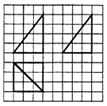 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为( )| A. | 136π | B. | 34π | C. | 25π | D. | 18π |
1.已知向量$\overrightarrow{a}$=(3,4),若λ$\overrightarrow{a}$=(3λ,2μ)(λ,μ∈R),且|λ$\overrightarrow{a}$|=5,则λ+μ=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | -1 |
19.等比数列{an}的前n项和为Sn,已知S1,2S2,3S3成等差数列,则{an}的公比为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
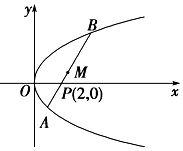 如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:
如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求: