题目内容
4.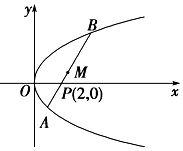 如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:
如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)P、M两点间的距离|PM|;
(2)线段AB的长|AB|.
分析 (1)求出直线l的参数方程,代入抛物线方程y2=2x,利用参数的几何意义求出P、M两点间的距离|PM|;
(2)利用参数的几何意义求出线段AB的长|AB|.
解答 解:(1)∵直线l过点P(2,0),斜率为$\frac{4}{3}$,
设直线的倾斜角为α,tanα=$\frac{4}{3}$,sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,
∴直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{3}{5}t}\\{y=\frac{4}{5}t}\end{array}\right.$ (t为参数).
∵直线l和抛物线相交,将直线的参数方程代入抛物线方程y2=2x中,
整理得8t2-15t-50=0,
则△=(-15)2-4×8×(-50)>0.
设这个二次方程的两个根分别为t1、t2,
由根与系数的关系,得t1+t2=$\frac{15}{8}$,t1t2=-$\frac{25}{4}$
由M为线段AB的中点,根据t的几何意义,得|PM|=$\frac{1}{2}$|t1+t2|=$\frac{15}{16}$
(2)|AB|=|t2-t1|=$\sqrt{\frac{225}{64}+4×\frac{25}{4}}$=$\frac{5}{8}\sqrt{73}$.
点评 本题考查直线与抛物线的位置关系,考查参数方程的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
15.张君四年前买了50000元的某种基金,收益情况是前两年每年递减20%,后两年每年递增20%,则现在的价值与原来价值比较,变化的情况是( )
| A. | 减少7.84% | B. | 增加7.84% | C. | 减少9.5% | D. | 增加 |
12.已知球O是的棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
19.如图所示,程序框图输出的结果是( )


| A. | 55 | B. | 89 | C. | 144 | D. | 233 |
16.命题“?x0∈R,$\frac{2}{{x}_{0}}$+lnx0≤0”的否定是( )
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
13.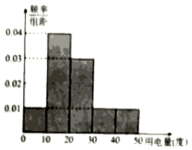 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
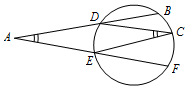 所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.
所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.