题目内容
17．将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D．则四面体ABCD的内切球的半径为（ ）| A． | 1 | B． | $2\sqrt{2}-\sqrt{3}$ | C． | $\sqrt{2}-1$ | D． | $2-\sqrt{3}$ |
分析 先求出VD-ABC，再求出四面体ABCD的表面积S=S△ADC+S△ABC+S△ABD+S△BCD，由四面体ABCD的内切球的半径r=$\frac{3{V}_{D-ABC}}{S}$，能求出结果．
解答 解：∵边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D，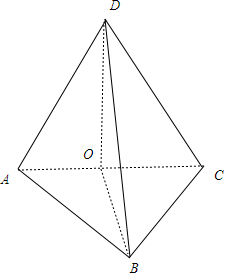
∴${S}_{△ABC}=\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1，AC=2，
取AC中点O，连结DO，BO，则DO=BO=$\sqrt{2-1}$=1，
且DO⊥平面ABC，
∴VD-ABC=$\frac{1}{3}×1×1$=$\frac{1}{3}$，
BD=$\sqrt{D{O}^{2}+B{O}^{2}}$=$\sqrt{2}$，AB=BC=AD=DC=$\sqrt{2}$，
∴${S}_{△ABD}={S}_{△BCD}=\frac{1}{2}×\sqrt{2}×\sqrt{2}×sin60°$=$\frac{\sqrt{3}}{2}$，
${S}_{△ADC}={S}_{△ABC}=\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1，
∴四面体ABCD的表面积S=S△ADC+S△ABC+S△ABD+S△BCD
=2+$\sqrt{3}$，
∴四面体ABCD的内切球的半径r=$\frac{3{V}_{D-ABC}}{S}$=$\frac{3×\frac{1}{3}}{2+\sqrt{3}}$=2-$\sqrt{3}$．
故选：D．
点评 本题考查四面体的内切球半径的求法，是中档题，解题时要认真审题，注意四面体内切球半径与其体积和表面积的关系式的合理应用．
练习册系列答案
相关题目
5．log${\;}_{\frac{1}{2}}$|x-$\frac{π}{3}$|≥log${\;}_{\frac{1}{2}}$$\frac{π}{2}$的解集为（ ）
| A． | {x|-$\frac{π}{6}$≤x≤$\frac{5}{6}$π} | B． | {x|x≤-$\frac{π}{6}$，或x≥$\frac{5}{6}$π} | ||
| C． | {x|-$\frac{π}{6}$≤x≤$\frac{5}{6}$π且x≠$\frac{π}{3}$} | D． | {x|-$\frac{5π}{6}$≤x≤$\frac{5π}{6}$且x≠$\frac{π}{3}$} |
12．已知球O是的棱长为1的正方体ABCD-A1B1C1D1的内切球，则平面ACD1截球O的截面面积为（ ）
| A． | π | B． | $\frac{π}{2}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$ |
2．
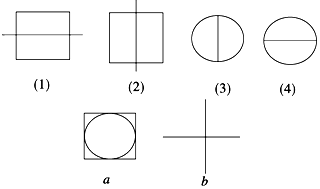定义A*B，B*C，C*D，D*A的运算分别对应下面图中的（1），（2），（3），（4），则图中，a，b对应的运算是（ ）
定义A*B，B*C，C*D，D*A的运算分别对应下面图中的（1），（2），（3），（4），则图中，a，b对应的运算是（ ）| A． | B*D，A*D | B． | B*D，A*C | C． | B*C，A*D | D． | C*D，A*D |
7．我们知道：在平面内，点（x0，y0）到直线Ax+By+C=0的距离公式为d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$，通过类比的方法，可求得：在空间中，点（2，4，1）到平面x+2y+3z+3=0的距离为（ ）
| A． | 3 | B． | 5 | C． | $\frac{8\sqrt{14}}{7}$ | D． | 3$\sqrt{5}$ |