题目内容
18.定义平面点集R2={x,y)|x∈R,y∈R丨,对于集合M⊆R2,若对?P0∈M,?r>0,使得{P∈R2||PP0|<r}⊆M,则称集合从为“开集”.给出下列命题:①集合{x,y)|(x-1)2+(y-3)2<1}是开集;
②集合{x,y)|x≥0,y>0}是开集;
③开集在全集R2上的补集仍然是开集;
④两个开集的并集是开集.
其中你认为正确的所有命题的序号是①④.
分析 根据新定义进行计算后判断,弄清开集的定义是解决本题的关键.即所选的集合需要满足存在以该集合内任意点为圆心,任意正实数为半径的圆内部分均在该集合内.初步确定该集合不含边界
解答 解:对于①,集合{x,y)|(x-1)2+(y-3)2<1}表示以点(0,3)为圆心,1为半径的圆面(不含边界),在该平面点集A中的任一点(x0,y0),则该点到圆周上的点的最短距离为d,取r=d,则满足,故正确;
对于②,在x=0,y>0的曲线上任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足条件,故错;
对于③,依题意可确定开集不含边界,开集在全集R2上的补集有边界,不是开集,故错;
对于④,两个开集的并集满足开集的定义,故正确.
故答案为:①④.
点评 本题属于集合的新定义型问题,考查学生即时掌握信息,解决问题的能力.正确理解好集的定义是解决本题的关键,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
13.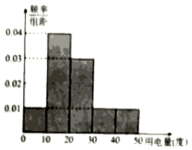 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
3.已知函数①f(x)=x2;②f(x)=ex③f(x)=lnx ④f(x)=cosx.其中对于f(x)定义域内的 任意一个xl都存在唯一的x2,使f(x1) f(x2)=l成立的函数是( )
| A. | ① | B. | ② | C. | ②③ | D. | ③④ |
7.我们知道:在平面内,点(x0,y0)到直线Ax+By+C=0的距离公式为d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,通过类比的方法,可求得:在空间中,点(2,4,1)到平面x+2y+3z+3=0的距离为( )
| A. | 3 | B. | 5 | C. | $\frac{8\sqrt{14}}{7}$ | D. | 3$\sqrt{5}$ |
8.设全集U=R,集合A={x|x>1},集合B={x|x>p},若(∁UA)∩B=∅,则p应该满足的条件是( )
| A. | p>1 | B. | p≥1 | C. | p<1 | D. | p≤1 |