题目内容
给出下列四个命题:
①?x∈R,x2+2x>4x-3;
②若log2x+logx2≥2,故x>1;
③命题“若a>b>0”,且c<0,则“
>
”的逆否命题是真命题;
④“a=1”是“直线x+y=0与直线x-ay=0互相垂直”的充分不必要条件,其中正确的命题为 (只填正确命题的序号)
①?x∈R,x2+2x>4x-3;
②若log2x+logx2≥2,故x>1;
③命题“若a>b>0”,且c<0,则“
| c |
| a |
| c |
| b |
④“a=1”是“直线x+y=0与直线x-ay=0互相垂直”的充分不必要条件,其中正确的命题为
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:对所给的命题进行逐个判断即可.
解答:
解:对于①:根据x2+2x>4x-3得
x2+2x-(4x-3>0,
∴x2-2x+3>0
∵△=4-12=-8<0,
∴解集为R,
∴该命题为真命题;
对于②:当log2x<0时,
则②不成立,
故该命题为假命题;
对于③:∵a>b>0,
∴
>
,
∵c<0,
∴
>
成立,
故该命题为真命题,根据原命题和其逆否命题真假性相同,
所以③为真命题;
对于④:直线x+y=0与直线x-ay=0互相垂直,
则1-a=0,
∴a=1,
∴“a=1”是“直线x+y=0与直线x-ay=0互相垂直”的充要条件,
∴④为真命题,
综上,真命题为:①③④.
故答案为:①③④.
x2+2x-(4x-3>0,
∴x2-2x+3>0
∵△=4-12=-8<0,
∴解集为R,
∴该命题为真命题;
对于②:当log2x<0时,
则②不成立,
故该命题为假命题;
对于③:∵a>b>0,
∴
| 1 |
| b |
| 1 |
| a |
∵c<0,
∴
| c |
| a |
| c |
| b |
故该命题为真命题,根据原命题和其逆否命题真假性相同,
所以③为真命题;
对于④:直线x+y=0与直线x-ay=0互相垂直,
则1-a=0,
∴a=1,
∴“a=1”是“直线x+y=0与直线x-ay=0互相垂直”的充要条件,
∴④为真命题,
综上,真命题为:①③④.
故答案为:①③④.
点评:本题重点考查了命题的真假判断、常用逻辑用语、充分条件、必要条件、充要条件等判断,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
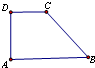 如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为
如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为