Question

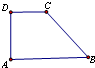如图，长沙梅溪湖有一块梯形湖面，AB、AD是两条互相垂直的环湖面的公路，CD、CB是两条环湖面的游览小道，且AB=200m，AD=CD=100m．现在A处有一夹角为

π

4

的探照灯，则探照灯能照射到的游览小道的最大值为

 

．

Answer 1

考点：函数的最值及其几何意义

专题：计算题,作图题,函数的性质及应用

分析：由题意设∠DAE=a，则0≤a≤

π

4

，从而可得CE+CF=100-100tana+100

2

tana=100+100（

2

-1）tana；从而求最大值．

解答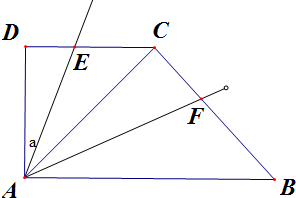： 解：设∠DAE=a，则0≤a≤

π

4

；
则DE=AD•tana=100tana；
AC=100

2

；
CF=ACtan∠CAF=100

2

tana；
则CE+CF=100-100tana+100

2

tana
=100+100（

2

-1）tana；
故当tana=1，即a=

π

4

时，
CE+CF有最大值，
最大值为100+100（

2

-1）=100

2

．
故答案为：100

2

m．

点评：本题考查了函数的最值的求法及三角函数的最值，属于中档题．