题目内容
圆O外一点P向圆引切线PC,切点为C,割线PAB,CD⊥PO于D点,已知∠POA=30°,则∠ABD= .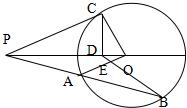

考点:与圆有关的比例线段
专题:立体几何
分析:根据切线的性质,结合射影定理可得:PC2=PD•PO,由切割线定理可得PC2=PA•PB,则PD•PO=PA•PB,即
=
,进而可判断△PAO∽△PDB,最后根据相似三角形的性质,可得∠ABD=∠PBD=∠POA.
| PB |
| PD |
| PO |
| PA |
解答:
解:∵PC为圆O的切线,故OC⊥PC,CD⊥PO,
由射影定理可得:PC2=PD•PO,
又由PAB是圆的割线,
∴PC2=PA•PB,
∴PD•PO=PA•PB,
即
=
,
在△PAO和△PDB中,
∠OPA=∠BPD,
∴△PAO∽△PDB,
∴∠ABD=∠PBD=∠POA=30°,
故答案为:30°
由射影定理可得:PC2=PD•PO,
又由PAB是圆的割线,
∴PC2=PA•PB,
∴PD•PO=PA•PB,
即
| PB |
| PD |
| PO |
| PA |
在△PAO和△PDB中,
∠OPA=∠BPD,
∴△PAO∽△PDB,
∴∠ABD=∠PBD=∠POA=30°,
故答案为:30°
点评:本题考查的知识点是与圆相关的比例线段,相似三角形的判定和性质,难度不大,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
若点A(m,1)在椭圆
+
=1的内部,则m的取值范围是( )
| x2 |
| 4 |
| y2 |
| 2 |
A、-
| ||||
B、m<-
| ||||
| C、-2<m<2 | ||||
| D、-1<m<1 |