��Ŀ����
10��ij�����ߴӵ����л�֪ij��˾���������з�֧����xi�� ���빫˾���������yi����ͳ��������������з���֧����xi��������yi��ͳ�Ʊ� ��λ����Ԫ
| ��� | ���з���֧����xi�� | ����yi�� |
| 2011 2012 2013 2014 2015 2016 | 5 11 4 5 3 2 | 31 40 30 34 25 20 |
| �ϼ� | 30 | 180 |
��2����x=xiʱ���ɻع�ֱ�߷���$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$�õ��ĺ���ֵ��Ϊ$\stackrel{��}{{y}_{i}}$�����ǽ���=|$\stackrel{��}{{y}_{i}}$-yi|��Ϊ��
�ڱ���6����������ȡ�������ݣ�������������������һ���������С��3�ĸ��ʣ�
�ο���ʽ������С���˷������Իع鷽�̵�ϵ����ʽ��
$\stackrel{��}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{��\overline x��}^2}}}}$=$\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-}\overline y��}}{{\sum_{i=1}^n{{{��x_i^{\;}-\overline x��}^2}}}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$��
���� ��1���������������ݣ�������С���˷���Ҫ��6�����ݣ������ݱ��ƽ�����������ݱ�Ļ��ĺͣ������ƽ���ͣ����빫ʽ���b��ֵ�������a��ֵ��д�����Իع鷽�̣�
��2���оٳ����еĻ����¼�����������������¼��ĸ��������̼��ɣ�
��� �⣺��1������������±���
| ��� | xi | yi | xi•yi | xi2 |
| 1 | 5 | 31 | 155 | 25 |
| 2 | 11 | 40 | 440 | 121 |
| 3 | 4 | 30 | 120 | 16 |
| 4 | 5 | 34 | 170 | 25 |
| 5 | 3 | 25 | 75 | 9 |
| 6 | 2 | 20 | 40 | 4 |
| $\overline{{x}_{i}}$=5 | $\overline{{y}_{i}}$=30 | $\sum_{i=1}^{6}$xi•yi=1000 | $\sum_{i=1}^{6}$xi2=200 |
��ع鷽���ǣ�$\widehat{y}$=2x+20����6�֣�
��2���������ݶ�Ӧ��������±���
| ��� | xi | yi | $\widehat{{y}_{i}}$ | �� |
| 1 | 5 | 31 | 30 | 1 |
| 2 | 11 | 40 | 42 | 2 |
| 3 | 4 | 30 | 28 | 2 |
| 4 | 5 | 34 | 30 | 4 |
| 5 | 3 | 25 | 26 | 1 |
| 6 | 2 | 20 | 24 | 4 |
��={��1��2������1��3������1��4������1��5������1��6������2��3������2��4������2��5������2��6������3��4������3��5������3��6������4��5������4��6������5��6��}
��15�������¼�
�¼���������һ��������ع�ֱ�߷�����õ��������С��3�������Ļ����¼��У���1��2������1��3������1��4������1��5������1��6������2��3������2��4������2��5������2��6������3��4������3��5������3��6������4��5������5��6������14�������¼�
��P=$\frac{14}{15}$
���ڱ���6����������ȡ�������ݣ�����������������һ��������ع�ֱ�߷�����õ��������С��3�ĸ���Ϊ$\frac{14}{15}$������12�֣�
���� ���⿼�����Իع������Ӧ�ã��������Ĺؼ���������С���˷������������Իع鷽�̵�ϵ��������������Ŀ���Եıر�������������һ���е��⣮

��ϰ��ϵ�д�
�����Ŀ
11����֪���ǵڶ����ǣ���sin��=$\frac{3}{5}$����cos����-����=��������
| A�� | $\frac{4}{5}$ | B�� | -$\frac{4}{5}$ | C�� | $\frac{3}{5}$ | D�� | -$\frac{3}{5}$ |
1����֪������R�ϵĺ���f��x��=$\left\{\begin{array}{l}{{x}^{2}-6ax-1��x��1}\\{{a}^{x}-7��x��1}\end{array}\right.$��������x1��x2������$\frac{f��{x}_{1}��-f��{x}_{2}��}{{x}_{1}-{x}_{2}}$��0����ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | ��$\frac{1}{3}$��1�� | B�� | [$\frac{1}{3}$��1�� | C�� | ��0��$\frac{1}{3}$�� | D�� | ��0��$\frac{1}{3}$] |
5������z=$\frac{3+2i}{i}$ ��iΪ������λ�����鲿Ϊ��������
| A�� | 3 | B�� | -3 | C�� | -3i | D�� | 2 |
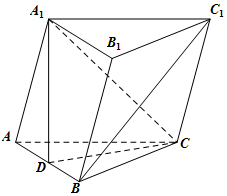 ��ͼ��������ABC-A1B1C1�У�AC=BC��AB=AA1����A1AB=60�㣬D��AB���е㣮
��ͼ��������ABC-A1B1C1�У�AC=BC��AB=AA1����A1AB=60�㣬D��AB���е㣮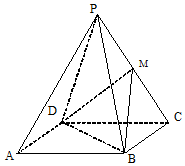 ��֪����P-ABCD�е����ı���ABCD�������Σ������涼�DZ߳�Ϊ2���������Σ�M����PC���е㣮�����ռ�ֱ������ϵ�����ÿռ�������������������⣺
��֪����P-ABCD�е����ı���ABCD�������Σ������涼�DZ߳�Ϊ2���������Σ�M����PC���е㣮�����ռ�ֱ������ϵ�����ÿռ�������������������⣺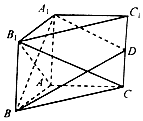 ��ͼ��ʾ��������A1B1C1-ABC�IJ���AA1�͵���ABC��AB��AC��AB=AA1��D����CC1���е㣮
��ͼ��ʾ��������A1B1C1-ABC�IJ���AA1�͵���ABC��AB��AC��AB=AA1��D����CC1���е㣮