题目内容
11.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,若在C上存在一点P,使得|PO|=$\frac{1}{2}$|F1F2|(O为坐标原点),且直线OP的斜率为$\sqrt{3}$,则,双曲线C的离心率为$\sqrt{3}$+1.分析 依题意可知|PO|=$\frac{1}{2}$|F1F2|判断出∠F1PF2=90°,直线OP的斜率为$\sqrt{3}$,可求出出|PF2|=$\sqrt{3}$c,则|F1P|=c,进而利用双曲线定义可用c表示出a,最后可求得双曲线的离心率.
解答 解:∵|PO|=$\frac{1}{2}$|F1F2|,
∴|OF1|=|OF2|=|OP|
∴∠F1PF2=90°,
∵直线OP的斜率为$\sqrt{3}$,
∴∠POF1=60°,
∴|PF1|=c,|PF2|=$\sqrt{3}$c,
∴$\sqrt{3}$c-c=2a,
∴$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1
∴e=$\sqrt{3}$+1.
故答案为:$\sqrt{3}$+1
点评 本题主要考查了双曲线的简单性质,考查了学生对双曲线定义的理解和灵活运用,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
1.已知定义在R上的函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-6ax-1,x≤1}\\{{a}^{x}-7,x>1}\end{array}\right.$,对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,则实数a的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | (0,$\frac{1}{3}$] |
6.在三棱锥P-ABC中,PA⊥平面ABC,PA=2$\sqrt{3}$,AC=2,AB=1,∠BAC=60°,则三棱锥P-ABC的外接球的表面积为( )
| A. | 13π | B. | 14π | C. | 15π | D. | 16π |
1.设 $a=ln\frac{1}{2},b={2^{\frac{1}{e}}},c={e^{-2}}$,则( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
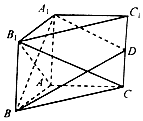 如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.
如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.