题目内容
5.设函数f(x)=$\left\{\begin{array}{l}{{x}^{3},x≤a}\\{{x}^{2},x>a}\end{array}\right.$.若存在实数b,使得函数y=f(x)-bx恰有2个零点,则实数a的取值范围是(-∞,0)∪(0,1).分析 令g(x)=$\frac{f(x)}{x}$,则只需让g(x)=b存在唯一一个非零解即可.讨论a的范围,作出g(x)的图象,根据图象判断即可得出结论.
解答 解:显然x=0必为f(x)-bx的一个零点,
当x≠0时,令f(x)-bx=0得b=$\frac{f(x)}{x}$,
令g(x)=$\frac{f(x)}{x}$=$\left\{\begin{array}{l}{{x}^{2},x≤a}\\{x,x>a}\end{array}\right.$,则b=g(x)存在唯一一个非零解.
当a<0时,作出g(x)的函数图象,如图所示: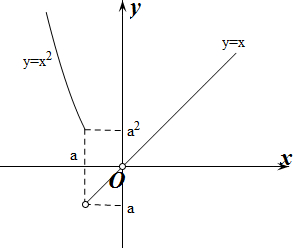
显然当a<b<a2且b≠0时,g(x)=b总存在唯一一个非零解,符合题意;
当a>0时,作出g(x)的函数图象如图所示: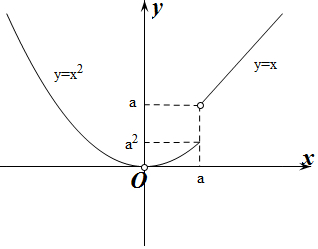
若要使b=g(x)存在唯一一个非零解,则a>a2,解得0<a<1.
同理,当a=0时,显然g(x)=b无非零解,
综上,a的取值范围是(-∞,0)∪(0,1).
故答案为:(-∞,0)∪(0,1).
点评 本题考查了函数零点与哈数图象的关系,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15.函数$f(x)=\left\{\begin{array}{l}-x+3a\\-{(x+1)^2}+2\end{array}\right.$$\begin{array}{l}x<0\\ x≥0\end{array}$,是R上的减函数,则a的取值范围是( )
| A. | (0,1) | B. | $[\frac{1}{3}$,+∞) | C. | (0,$\frac{1}{3}]$ | D. | (0,$\frac{2}{3}]$ |
16.一个总体中有600个个体,随机编号为001,002,…,600,利用系统抽样方法抽取容量为24的一个样本,总体分组后在第一组随机抽得的编号为006,则在编号为051~125之间抽得的编号为( )
| A. | 056,080,104 | B. | 054,078,102 | C. | 054,079,104 | D. | 056,081,106 |
10.执行如图所示的程序框图,若输入n=5,则输出的S值为( )
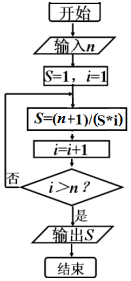

| A. | $\frac{1}{20}$ | B. | $\frac{5}{16}$ | C. | $\frac{16}{5}$ | D. | $\frac{3}{8}$ |
17.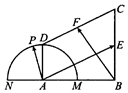 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )
 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )| A. | [-2,2] | B. | $[{-2,2\sqrt{2}}]$ | C. | $[{-2\sqrt{2},2}]$ | D. | $[{-2\sqrt{2},2\sqrt{2}}]$ |
14.在极坐标系中,曲线C:sinθ=|cosθ|上不同的两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,则|MN|=( )
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |