Question

13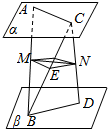．如图，设平面α∥平面β，AB、CD是两异面直线，且A、C∈α，B、D∈β，AC⊥BD，AC=6，BD=8，M是AB的中点，过点M作一个平面γ，交CD于N，交BC于E，且γ∥α∥β，求线段MN的长．

Answer 1

分析 根据平面与平面平行的性质、三角形中位线定理可以得到△MEN是直角三角形，则利用勾股定理可以来求MN的长度．

解答 证明：由题意得到：ME是△ABC的中位线，则ME∥AC，且ME=$\frac{1}{2}$AC=3．
EN是△BCD的中位线，则EN∥BD，且EN=$\frac{1}{2}$BD=4，
∵AC⊥BD，
∴ME⊥EN，
∴MN=$\sqrt{M{E}^{2}+N{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5．即MN的长度是5．

点评 本题考查平面与平面平行的判定，考查学生逻辑思维能力，空间想象能力，是中档题．