题目内容
1.已知a,b,c这三个实数中至少有一个不等于1,试比较a2+b2+c2与2a+2b+2c-3的大小.分析 作差,配方即可比较大小.
解答 解:a2+b2+c2-(2a+2b+2c-3)
=a2-2a+1+b2-2b+1+c2-2c+1
=(a-1)2+(b-1)2+(c-1)2.
∵a,b,c这三个数中至少有一个不等于1,
∴a-1,b-1,c-1中至少有一个不为0.
(a-1)2+(b-1)2+(c-1)2>0.
∴a2+b2+c2>2a+2b+2c-3..
点评 本题考查作差法比较大小,关键是配方,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.函数f(x)=$\frac{lnx}{x}$-a在区间(1,2)内有零点,则实数a的取值范围是( )
| A. | (-$\frac{ln3}{2}$,-$\frac{ln2}{2}$) | B. | (0,$\frac{ln2}{2}$) | C. | ($\frac{ln2}{2}$,$\frac{ln3}{2}$) | D. | ($\frac{ln2}{2}$,+∞) |
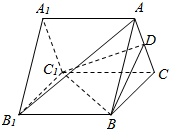 如图所示,已知A1B1C1-ABC是正三棱柱(底面是正三角形,侧棱与底面垂直),D是AC的中点.
如图所示,已知A1B1C1-ABC是正三棱柱(底面是正三角形,侧棱与底面垂直),D是AC的中点. 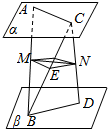 如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.
如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.