题目内容

5．若3x-2y=2，则$\frac{2{5}^{y}}{{5}^{3x}}$=$\frac{1}{25}$．

分析 由3x-2y=2可得：2y-3x=-2．结合指数的运算性质，可得答案．

解答 解：∵3x-2y=2，
∴2y-3x=-2．
∴$\frac{2{5}^{y}}{{5}^{3x}}$=$\frac{{5}^{2y}}{{5}^{3x}}$=52y-3x=5-2=$\frac{1}{25}$，
故答案为：$\frac{1}{25}$

点评 本题考查的知识点是有理数指数幂的化简与求值，熟练掌握指数的运算性质，是解答的关键．

练习册系列答案
相关题目
15．已知全集U={x|-x2+3x≤2}，A={x|y=$\frac{1}{\sqrt{{x}^{2}-4x+3}}$}，B={x|x＞2或x≤1}求
（1）A∩∁UB；
（2）（∁UA∪B）∩A．
16．函数f（x）=$\frac{lnx}{x}$-a在区间（1，2）内有零点，则实数a的取值范围是（　　）
A．（-$\frac{ln3}{2}$，-$\frac{ln2}{2}$）B．（0，$\frac{ln2}{2}$）C．（$\frac{ln2}{2}$，$\frac{ln3}{2}$）D．（$\frac{ln2}{2}$，+∞）
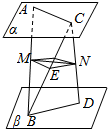13．如图，设平面α∥平面β，AB、CD是两异面直线，且A、C∈α，B、D∈β，AC⊥BD，AC=6，BD=8，M是AB的中点，过点M作一个平面γ，交CD于N，交BC于E，且γ∥α∥β，求线段MN的长．
20．小王计划采用等额本息分期付款的方式购买一台，售价为4000元的笔记本电脑，年利率为5.76%，三年还清贷款，问每月需要付多少贷款？
10．已知定义在R上的偶函数，f（x）在x≥0时，f（x）=ex+1n（x+1），若 f（a）＜f（a-1），则a的取值范围是（-∞，$\frac{1}{2}$）．
17．已知x＞1，则xlnlnx-（lnx）lnx的值是（　　）
A．正数B．零C．负数D．不能确定
14．已知tanα，tanβ是关于x的方程x2-4px-3=0（p∈R）的两个实数根，且α+β≠kπ+$\frac{π}{2}$（k∈Z），求cos2（α+β）+psin（α+β）cos（α+β）的值．
15．函数f（x）=a-x-logax（a＞0，a≠1）的零点的个数为（　　）
A．0B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网