题目内容
2.已知函数f(x)=2sin2x+2$\sqrt{3}$sinx•sin(x+$\frac{π}{2}$)(ω>0).(1)求f(x)的最小正周期;
(2)求函数f(x)在区间[0,$\frac{2π}{3}$]上的取值范围.
分析 (1)由三角函数公式化简可得f(x)=1+2sin(2x-$\frac{π}{6}$),由周期公式可得;
(2)由x∈[0,$\frac{2π}{3}$]结合三角函数的性质可得取值范围.
解答 解:(1)由三角函数公式化简可得
f(x)=2sin2x+2$\sqrt{3}$sinx•sin(x+$\frac{π}{2}$)
=2sin2x+2$\sqrt{3}$sinx•cosx
=1-cos2x+$\sqrt{3}$sin2x
=1+2sin(2x-$\frac{π}{6}$)
∴f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)∵x∈[0,$\frac{2π}{3}$],∴2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{7π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴2sin(2x-$\frac{π}{6}$)∈[-1,2],
∴1+2sin(2x-$\frac{π}{6}$)∈[0,3],
∴函数f(x)在区间[0,$\frac{2π}{3}$]上的取值范围为:[0,3]
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和值域,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知x>1,则xlnlnx-(lnx)lnx的值是( )
| A. | 正数 | B. | 零 | C. | 负数 | D. | 不能确定 |
12.将下列各式按大小顺序排列,其中正确的是( )
| A. | cos0°<cos$\frac{1}{2}$<cos1<cos30°<cosπ° | B. | cos0°<cosπ°<cos$\frac{1}{2}$cos30°<cos1 | ||
| C. | cos0°>cos$\frac{1}{2}$>cos1>cos30°>cosπ° | D. | cos0°>cosπ°>cos$\frac{1}{2}$>cos30°>cos1 |
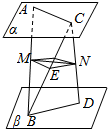 如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.
如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.