题目内容
3.已知函数f(x)=ax,(a>0且a≠1).(Ⅰ)当a=2时,若函数g(x)=$\left\{\begin{array}{l}{-x+m,x<1}\\{f(x),x≥1}\end{array}\right.$ 的最小值为2,求实数m的取值范围;
(Ⅱ)若函数f(x)在区间[-1,1]上的图象位于直线y=2的下方,求a的取值范围.
分析 (Ⅰ)当a=2时,函数g(x)=$\left\{\begin{array}{l}-x+m,x<1\\{2}^{x},x≥1\end{array}\right.$,结合函数最小值为2,可得m-1≥2,解得实数m的取值范围;
(Ⅱ)若函数f(x)在区间[-1,1]上的图象位于直线y=2的下方,则$\left\{\begin{array}{l}{a}^{-1}<2\\ a<2\end{array}\right.$,解得a的取值范围.
解答 解:(Ⅰ)当a=2时,函数g(x)=$\left\{\begin{array}{l}-x+m,x<1\\{2}^{x},x≥1\end{array}\right.$,
当x<1时,g(x)>m-1,
当x≥1时,g(x)≥2,
若函数g(x) 的最小值为2,则m-1≥2,
∴m∈[3,+∞)
(Ⅱ)若函数f(x)在区间[-1,1]上的图象位于直线y=2的下方,
则$\left\{\begin{array}{l}{a}^{-1}<2\\ a<2\end{array}\right.$,
解得:a∈($\frac{1}{2}$,1)∪(1,2)
点评 本题考查的知识点是分段函数的应用,函数的最值,指数函数的图象和性质,难度中档.

练习册系列答案
相关题目
13.y=$\sqrt{1-x}+{log_2}$(x+1)的定义域是( )
| A. | [-1,1] | B. | [-1.1) | C. | (-1,1) | D. | (-1,1] |
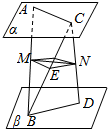 如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.
如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.