题目内容
已知（2+
）n（其中n∈N*）的展开式中含x3项的系数为14，则n=（ ）
| x |
| A、6 | B、7 | C、8 | D、9 |
考点：二项式系数的性质
专题：二项式定理
分析：在二项展开式的通项公式中，令x的幂指数等于3，求出r的值，即可求得含x3项的系数，再根据含x3项的系数等于14求得n的值．
解答：
解：（2+
）n（其中n∈N*）的展开式的通项公式为Tr+1=
•2n-r•(
)r，
令
=3，求得r=6，可得展开式中含x3项的系数为
•2n-6=14，
由于n≥6，结合所给的选项，n=7满足条件，
故选：B．
| x |
| C | r n |
| x |
令
| r |
| 2 |
| C | 6 n |
由于n≥6，结合所给的选项，n=7满足条件，
故选：B．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
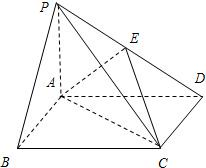如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4．E是PD的中点，
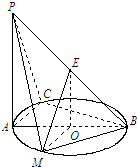如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA=30°，PA=AB=2，点E为线段PB的中点，点M在弧AB上，且OM∥AC．