题目内容
已知函数f(x)=
x3-ax2+(a2-1)x+b,其图象在点(1,f(x))处的切线方程为x+y-3=0.
(1)求a,b的值与函数f(x)的单调区间;
(2)若对x∈[-2,4],不等式f(x)<c2-c恒成立,求c的取值范围.
| 1 |
| 3 |
(1)求a,b的值与函数f(x)的单调区间;
(2)若对x∈[-2,4],不等式f(x)<c2-c恒成立,求c的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由已知可得f′(x)=x2-2ax+(a2-1),f(1)=2=
-a+a2-1+b,利用导数的几何意义可得f′(1)=1-2a+a2-1=-1,联立解得即可.
(2)利用导数可得出函数的单调性极值与最值,由x∈[-2,4],不等式f(x)<c2-c恒成立?[f(x)]max<c2-c,x∈[-2,4].解出即可.
| 1 |
| 3 |
(2)利用导数可得出函数的单调性极值与最值,由x∈[-2,4],不等式f(x)<c2-c恒成立?[f(x)]max<c2-c,x∈[-2,4].解出即可.
解答:
解:(1)f(x)=
x3-ax2+(a2-1)x+b,
∴f′(x)=x2-2ax+(a2-1),
∵函数f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0.
∴f(1)=2=
-a+a2-1+b,f′(1)=1-2a+a2-1=-1,
解得a=1,b=
.
∴f′(x)=x2-2x=x(x-2),
令f′(x)>0,解得x>2或x<0;令f′(x)<0,解得0<x<2.
∴函数f(x)的单调递增为(-∞,0),(2,+∞);单调递减区间为(0,2).
(2)由(1)可得:f(x)=
x3-x2+
,f′(x)=x2-2x=x(x-2).
由表格可知:当x=0时,函数f(x)取得极大值,f(0)=
,又f(4)=8.
∴函数f(x)在x∈[-2,4]上的最大值为8.
由x∈[-2,4],不等式f(x)<c2-c恒成立?[f(x)]max<c2-c,x∈[-2,4].
∴c2-c>8,
解得c>
或c<
.
∴c的取值范围是(-∞,
)∪(
,+∞).
| 1 |
| 3 |
∴f′(x)=x2-2ax+(a2-1),
∵函数f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0.
∴f(1)=2=
| 1 |
| 3 |
解得a=1,b=
| 8 |
| 3 |
∴f′(x)=x2-2x=x(x-2),
令f′(x)>0,解得x>2或x<0;令f′(x)<0,解得0<x<2.
∴函数f(x)的单调递增为(-∞,0),(2,+∞);单调递减区间为(0,2).
(2)由(1)可得:f(x)=
| 1 |
| 3 |
| 8 |
| 3 |
| x | [-2,0) | 0 | (0,2) | 2 | (2,4] |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
| 8 |
| 3 |
∴函数f(x)在x∈[-2,4]上的最大值为8.
由x∈[-2,4],不等式f(x)<c2-c恒成立?[f(x)]max<c2-c,x∈[-2,4].
∴c2-c>8,
解得c>
1+
| ||
| 2 |
1-
| ||
| 2 |
∴c的取值范围是(-∞,
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题考查了利用导数可得出函数的单调性极值与最值、切线方程,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知(2+
)n(其中n∈N*)的展开式中含x3项的系数为14,则n=( )
| x |
| A、6 | B、7 | C、8 | D、9 |
已知△ABC面积为1,点P满足
=
+
,在△ABC内任取M,那么落入△BPC内的概率为( )
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,他等待的时间不多于10分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
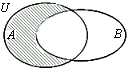 已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )| A、{x|1≤x<3} |
| B、{x|x<3} |
| C、{x|x≤-1} |
| D、{x|-1<x<1} |
已知直线l1:3x-(k+2)y+6=0与直线l2:kx+(2k-3)y+2=0,记
.D=0是两条直线l1与直线l2平行的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |