题目内容
已知从一点P引出三条射线PA、PB、PC,且两两成角60°,则二面角B-PA-C的余弦值是 .
考点:二面角的平面角及求法
专题:空间角
分析:运用题目的条件得出∠BEC为二面角B-PA-C的平面角,△BEC中,BE=CE=
,BC=2,运用余弦定理求解即可得出cos∠BEC=
=
,
| 3 |
| 3+3-4 | ||||
2×
|
| 1 |
| 3 |
解答:
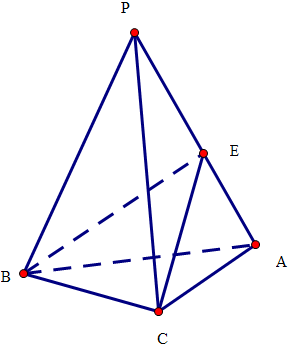 解:从一点P引出三条射线PA、PB、PC,且两两成角60°,
解:从一点P引出三条射线PA、PB、PC,且两两成角60°,
取PA=PB=PC=2,PE=1,连接BE,CE
∵∠BPE=∠CPE=60°,
∴△PBE≌△PCE,
∴BE=CE,
根据余弦定理得出:BE=CE=
=
,
∴根据勾股定理判断出BE⊥PE,CE⊥PE,
∠BEC为二面角B-PA-C的平面角,
∵△BEC中,BE=CE=
,BC=2,
∴cos∠BEC=
=
,
故答案为:
.
 解:从一点P引出三条射线PA、PB、PC,且两两成角60°,
解:从一点P引出三条射线PA、PB、PC,且两两成角60°,取PA=PB=PC=2,PE=1,连接BE,CE
∵∠BPE=∠CPE=60°,
∴△PBE≌△PCE,
∴BE=CE,
根据余弦定理得出:BE=CE=
4+1-2×2×1×
|
| 3 |
∴根据勾股定理判断出BE⊥PE,CE⊥PE,
∠BEC为二面角B-PA-C的平面角,
∵△BEC中,BE=CE=
| 3 |
∴cos∠BEC=
| 3+3-4 | ||||
2×
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,其中求出二面角的平面角转化为三角形中求解是解答本题的关键.

练习册系列答案
相关题目
已知(2+
)n(其中n∈N*)的展开式中含x3项的系数为14,则n=( )
| x |
| A、6 | B、7 | C、8 | D、9 |
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,他等待的时间不多于10分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
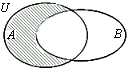 已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )| A、{x|1≤x<3} |
| B、{x|x<3} |
| C、{x|x≤-1} |
| D、{x|-1<x<1} |