题目内容
在实数集R内，我们用“＜”为全体实数排了一个“序”，类似的，我们在向量集上也可以定义一个“序”的关系，记为“?”，定义如下：对于任意两个向量
=（x1，y1）•（x1，y1∈R），
=（x2，y2）•（x2，y2∈R），当取仅当“x1＜x2“或“x1=x2且y1＜y2∈R”时，
?
，按上述定义的关系“?”，给出如下四个命题：
①若
?
，则|
|≤|
|；
②若
?
，
?
，则，则
?
；
③若
?
，则对于任意
，都有（
+
）?（
+
）成立；
④对于实数λ≥0，若
?
，则λ
?λ
成立；
其中所有命题的个数为（ ）
| m1 |
| m2 |
| m1 |
| m2 |
①若
| m1 |
| m2 |
| m1 |
| m2 |
②若
| m1 |
| m2 |
| m2 |
| m3 |
| m1 |
| m3 |
③若
| m1 |
| m2 |
| m |
| m1 |
| m |
| m2 |
| m |
④对于实数λ≥0，若
| m1 |
| m2 |
| m1 |
| m2 |
其中所有命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：平面向量数量积的运算
专题：新定义,平面向量及应用
分析：根据已知条件中，对于任意两个向量
=（x1，y1）•（x1，y1∈R），
=（x2，y2）•（x2，y2∈R），当取仅当“x1＜x2“或“x1=x2且y1＜y2∈R”时，
?
，按上述定义的关系“?”，判断各个选项是否正确，从而得出结论．
| m1 |
| m2 |
| m1 |
| m2 |
解答：
解：对于任意两个向量
=（x1，y1）•（x1，y1∈R），
=（x2，y2）•（x2，y2∈R），当取仅当“x1＜x2“或“x1=x2且y1＜y2∈R”时，
?
，按上述定义的关系“?”．
对于①若
?
，则“x1＜x2“或“x1=x2且y1＜y2∈R”，|
|=
，|
|=
，
不一定有|
|≤|
|，故①不正确；
对于②，设向量
=（x1，y1），
=（x2，y2），
=（x3，y3），若
?
，
?
，
则有“x1＜x2”或“x1=x2且y1＜y2”，“x2＜x3”或“x2=x3且y2＜y3”．
故有“x1＜x3”或“x1=x3且y1＜y3”．故有
?
，故②正确；
对于③，若
?
，则对于任意
，设
=（x，y），
=（x1，y1），
=（x2，y2），
由于“x1＜x2”或“x1=x2且y1＜y2”，则“x+x1＜x+x2”或“x+x1=x+x2且y+y1＜y+y2”，
即有（
+
）?（
+
）成立，故③正确；
对于④，对于实数λ≥0，设向量
=（x1，y1），
=（x2，y2），若
?
，
则有“x1＜x2”或“x1=x2且y1＜y2”，即有“λx1≤λx2”或“λx1=λx2且λy1≤λy2”，
则λ
?λ
不成立，故④不正确．
综上正确的个数为2．
故选B．
| m1 |
| m2 |
| m1 |
| m2 |
对于①若
| m1 |
| m2 |
| m1 |
| x12+y12 |
| m2 |
| x22+y22 |
不一定有|
| m1 |
| m2 |
对于②，设向量
| m1 |
| m2 |
| m3 |
| m1 |
| m2 |
| m2 |
| m3 |
则有“x1＜x2”或“x1=x2且y1＜y2”，“x2＜x3”或“x2=x3且y2＜y3”．
故有“x1＜x3”或“x1=x3且y1＜y3”．故有
| m1 |
| m3 |
对于③，若
| m1 |
| m2 |
| m |
| m |
| m1 |
| m2 |
由于“x1＜x2”或“x1=x2且y1＜y2”，则“x+x1＜x+x2”或“x+x1=x+x2且y+y1＜y+y2”，
即有（
| m1 |
| m |
| m2 |
| m |
对于④，对于实数λ≥0，设向量
| m1 |
| m2 |
| m1 |
| m2 |
则有“x1＜x2”或“x1=x2且y1＜y2”，即有“λx1≤λx2”或“λx1=λx2且λy1≤λy2”，
则λ
| m1 |
| m2 |
综上正确的个数为2．
故选B．
点评：本题以命题的真假判断为载体，考查了新定义“?”，正确理解新定义“?”的实质，是解答的关键，属于中档题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
若-
＜α＜-
，从单位圆中的三角函数线观察sinα，cosα，tanα的大小是（ ）
| 3π |
| 4 |
| π |
| 2 |
| A、sinα＜tanα＜cosα |
| B、cosα＜sinα＜tanα |
| C、sinα＜coasα＜tanα |
| D、tanα＜sinα＜cosα |
已知直线a∥平面α，直线a⊥平面β，则（ ）
| A、α⊥β | B、α∥β |
| C、α与β不垂直 | D、以上都有可能 |
在函数f（x）=
，则f（log310）=（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
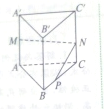如图，在直棱柱ABC-A′B′C′中，底面是边长为3的等边三角形，AA′=4，M为AA′的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC′到M的最短路线长为
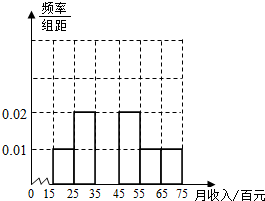为了解某市民众对某项公共政策的态度，在该市随机抽取了50名市民进行调查，做出了他们的月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到他们月收入情况以及对该项政策赞成的人数统计表：