题目内容
10.如图是一个棱锥的正视图和侧视图,则该棱锥的俯视图可能是( )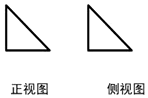
| A. |  | B. |  | C. | 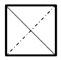 | D. |  |
分析 根据已知中的正视图和侧视图,分析出俯视图可能出现的情况,可得答案.
解答 解:若几何体为三棱锥,由其正视图和侧视图可知,
其底面在下方,且为直角三角形,C答案符号要求;
若几何体为四棱锥,由其正视图和侧视图可知,
其底面在下方,且为正方形,对角线应从左上到右下,不存在满足条件的答案;
故选:C
点评 本题考查的知识点是简单空间图形的三视图,空间想象能力,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.甲、乙两人玩一种游戏,游戏规则如下:先将筹码放在如下表的正中间D处,投掷一枚质地均匀的硬币,若正面朝上,筹码向右移动一格;若反面朝上,筹码向左移动一格.
(1)将硬币连续投掷三次,现约定:若筹码停在A或B或C或D处,则甲赢;否则,乙赢.问该约定对乙公平吗?请说明理由.
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定:
①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A-G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.
| A | B | C | D | E | F | G |
| 30 | 5 | 10 | 10 | 5 | 20 | 30 |
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定:
①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A-G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.
5.设复数z=$\frac{2i}{1+i}$,则其共轭复数为( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |
2.设U=R,A={x|2x<2},B={x|log2x<0},则A∩(∁UB)=( )
| A. | ∅ | B. | {x|x≤0} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )


| A. | f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)在[-$\frac{π}{3}$,0]上单调递增 | |
| C. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| D. | 将函数y=2sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{6}$个单位得到f(x)的图象 |