题目内容
已知椭圆E:
+
=1(a>b>0)的左、右顶点分别为A1,A2,左焦点为F,动直线x=m(|m|<a)与E相交于P,Q两点,A1P与A2Q的交点M的轨迹落在双曲线
-y2=1上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过F点的直线l与E相交A、B两点,与圆x2+y2=a2相交于C、D两点,求
的范围.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)过F点的直线l与E相交A、B两点,与圆x2+y2=a2相交于C、D两点,求
| |AB| |
| |CD| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意设M(x,y),P(x0,y0),Q(x0,-y0),由已知条件推导出M的轨迹M(x,y)的轨迹方程为
-
=1,由此能求出椭圆方程.
(Ⅱ)设A(x1,y1),B(x2,y2),将AB:x=my-1代入椭圆方程得(m2+2)y2-2my-1=0,由此利用换元法和导数性质能求出
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅱ)设A(x1,y1),B(x2,y2),将AB:x=my-1代入椭圆方程得(m2+2)y2-2my-1=0,由此利用换元法和导数性质能求出
| |AB| |
| |CD| |
解答:
解:(Ⅰ)由题意设M(x,y),P(x0,y0),Q(x0,-y0),
则A1P:y=
(x+a)(1),A2Q:y=
(x-a)(2),
将方程(1)(2)相乘得y2=-
(x2-a2)…(3分)
∵P(x0,y0)在椭圆上,
∴y02=
(a2-x02),
代入上式,得y2=
(x2-a2),
∴M(x,y)的轨迹方程为
-
=1.
又∵M的轨迹在双曲线
-y2=1上,
∴所求的椭圆方程为
+y2=1.…(6分)
(Ⅱ)设A(x1,y1),B(x2,y2),
将AB:x=my-1代入椭圆方程得(m2+2)y2-2my-1=0,
∴|AB|=
|y1-y2|=
=2
.…(8分)
而|CD|=2
=2
.
∴λ=
=
. …(9分)
令t=
,t∈[0,1](AB为x轴时,m不存在,
此时t=0,λ=
.
∵函数f(x)=-x3+3x+2,
∴f′(x)=-3x2+3,
由f′(x)=-3x2+3<0,得-1<x<1,
∴函数f(x)=-x3+3x+2在[-1,1]上递减,
∴t=0,即m不存在时,λmax=1,t=1,即m=0时,λmin=
.
∴
的取值范围是[
, 1].…(12分)
则A1P:y=
| y0 |
| x0+a |
| -y0 |
| x0-a |
将方程(1)(2)相乘得y2=-
| y02 |
| x02-a2 |
∵P(x0,y0)在椭圆上,
∴y02=
| b2 |
| a2 |
代入上式,得y2=
| b2 |
| a2 |
∴M(x,y)的轨迹方程为
| x2 |
| a2 |
| y2 |
| b2 |
又∵M的轨迹在双曲线
| x2 |
| 2 |
∴所求的椭圆方程为
| x2 |
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),
将AB:x=my-1代入椭圆方程得(m2+2)y2-2my-1=0,
∴|AB|=
| 1+m2 |
| 1+m2 |
2
| ||
| m2+2 |
| 2 |
| m2+1 |
| m2+2 |
而|CD|=2
2-
|
|
∴λ=
| |AB| |
| |CD| |
| 2 |
|
令t=
| 1 |
| m2+1 |
此时t=0,λ=
| ||
|
∵函数f(x)=-x3+3x+2,
∴f′(x)=-3x2+3,
由f′(x)=-3x2+3<0,得-1<x<1,
∴函数f(x)=-x3+3x+2在[-1,1]上递减,
∴t=0,即m不存在时,λmax=1,t=1,即m=0时,λmin=
| ||
| 2 |
∴
| |AB| |
| |CD| |
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查两条线段比值的取值范围的求法,解题时要注意导数性质的合理运用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
若实数x,y满足
,则z=3x+2y的最大值是( )
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |
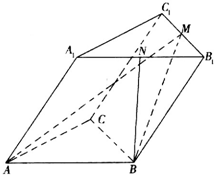 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°. 在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.
在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.