题目内容
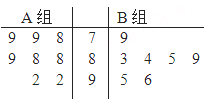 天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.(Ⅰ)若在确定为优秀厂家的厂家中随机抽取2家进行复查,求抽取的2家进行复查的分别是A、B组评定出的优秀厂家各1个的概率;
(Ⅱ)若从A、B两组评定出确定为优秀厂家中随机选取3家人户,记选取的3家来自B组评定出的优秀厂家数为ξ,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,茎叶图
专题:概率与统计
分析:(I)由题意先求出平均数,再判断符合满足条件的优秀厂家数,由此能求出抽取的两家评出的优秀厂家个1个的概率.
(II)从题意中获知ξ的取值可为0,1,2,3.发生对应事件的概率为P(ξ=k)=
,由此能ξ的分布列和数学期望.
(II)从题意中获知ξ的取值可为0,1,2,3.发生对应事件的概率为P(ξ=k)=
| ||||
|
解答:
解:(I)由题意得:
=
=86
符合满足上述条件的优秀厂家数:7个;其中A组4个,B组3个;
∴抽取的两家评出的优秀厂家个1个的概率为P=
=
.…(6分)
(II)从题意中获知ζ的取值可为0,1,2,3.
发生对应事件的概率为P(ξ=k)=
,k=0,1,2,3,
∴P(ξ=0)=
=
;
P(ξ=1)=
=
;
P(ζ=2)=
=
;
P(ξ=3)=
=
∴ξ的分布列如表:
∴E(ζ)=0×
+1×
+2×
+3×
=
.…(12分)
. |
| x |
| 78+79×3+83×2+84+85×2+88+89×2+92×2+95+96 |
| 16 |
符合满足上述条件的优秀厂家数:7个;其中A组4个,B组3个;
∴抽取的两家评出的优秀厂家个1个的概率为P=
| ||||
|
| 4 |
| 7 |
(II)从题意中获知ζ的取值可为0,1,2,3.
发生对应事件的概率为P(ξ=k)=
| ||||
|
∴P(ξ=0)=
| ||||
|
| 4 |
| 35 |
P(ξ=1)=
| ||||
|
| 18 |
| 35 |
P(ζ=2)=
| ||||
|
| 12 |
| 35 |
P(ξ=3)=
| ||||
|
| 1 |
| 35 |
∴ξ的分布列如表:
| ζ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 4 |
| 35 |
| 18 |
| 35 |
| 12 |
| 35 |
| 1 |
| 35 |
| 9 |
| 7 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
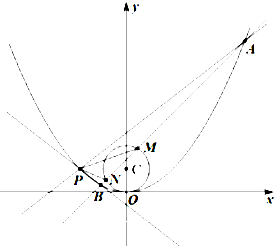 设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.
设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.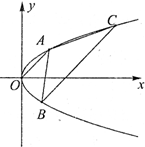 已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.
已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.