题目内容
已知tanx=5，则
=（ ）
| sinx+3cosx |
| sinx-cosx |
| A、1 | B、2 | C、3 | D、4 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：把要求的式子利用同角三角函数的基本关系化为
，再把tanx=5代入运算求得结果．
| tanx+3 |
| tanx-1 |
解答：
解：∵tanx=5，则
=
=
=2，
故选：B．
| sinx+3cosx |
| sinx-cosx |
| tanx+3 |
| tanx-1 |
| 5+3 |
| 5-1 |
故选：B．
点评：本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
相关题目
设随机变量X服从正态分布N（3，4），若P（X＜2a+3）=P（X＞a-2），则a的值为（ ）
A、
| ||
| B、3 | ||
| C、5 | ||
D、
|
设等差数列{an}的前n项和Sn，若S13=26，S14=-14，则Sn取最大值时，n的值为（ ）
| A、7 | B、8 | C、9 | D、14 |
下列选项中，p是q的必要不充分条件是（ ）
| A、p：a+c＞b+d；q：a＞b，且c＞d | ||||
| B、p：x=0；q：x2=x | ||||
| C、p：a＞1；q：y=ax（a＞0且a≠1）在R上为增函数 | ||||
D、p：α=
|
已知圆C的内接正三角形的边长为
，且圆心为直线x-y+1=0与x轴的交点，则圆C的方程为（ ）
| 3 |
| A、（x-1）2+y2=1 |
| B、（x-1）2+y2=4 |
| C、（x+1）2+y2=1 |
| D、（x+1）2+y2=4 |
若一束光线从点P（1，0）射出后，经直线x-y+1=0反射后恰好过点Q（2，1），在这一过程中，光线从P到Q所经过的最短路程是（ ）
A、2
| ||
B、2+
| ||
C、
| ||
D、2+
|
已知
，
为非零向量，则“|
+
|=|
|+|
|”是“
∥
”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
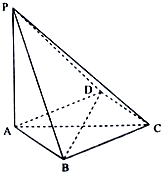如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA=AB=2，∠BAD=60°．