题目内容
若关于x的不等式（x2-1）•（x-a）＜0没有正整数解，则实数a的最大值为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：由（x2-1）•（x-a）=0，可得x=±1，a．当a＞1时，不等式的解集是{x|x＜-1或1＜x＜a}，当a＞2时，关于x的不等式（x2-1）•（x-a）＜0有正整数解，因此只考虑1＜a≤2时即可．
解答：
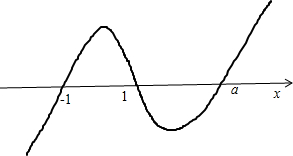解：由（x2-1）•（x-a）=0，可得x=±1，a．
当a＞1时，不等式（x2-1）•（x-a）＜0的解集是{x|x＜-1或1＜x＜a}，
可知：当1＜a≤2时，关于x的不等式（x2-1）•（x-a）＜0没有正整数解，
当a＞2时，不等式（x2-1）•（x-a）＜0有正整数解，不符合题意，应舍去．
∵要求的是实数a的最大值，∴当a≤1时，不必考虑．
综上可得：实数a的最大值为2．
故选：B．
解：由（x2-1）•（x-a）=0，可得x=±1，a．当a＞1时，不等式（x2-1）•（x-a）＜0的解集是{x|x＜-1或1＜x＜a}，
可知：当1＜a≤2时，关于x的不等式（x2-1）•（x-a）＜0没有正整数解，
当a＞2时，不等式（x2-1）•（x-a）＜0有正整数解，不符合题意，应舍去．
∵要求的是实数a的最大值，∴当a≤1时，不必考虑．
综上可得：实数a的最大值为2．
故选：B．
点评：本题考查了一元二次不等式的解法，考查了分类讨论的思想方法，考查了推理能力，属于难题．
练习册系列答案
相关题目
若f（x）=ax3+bx2+cx+d（a＞0），则函数f（x）在R上为增函数的充要条件为（ ）
| A、b2＜3ac |
| B、b2＞3ac |
| C、b2≤3ac |
| D、b2≥3ac |
已知△ABC的内角为A，B，C，且2
sin2
=sinC+
，则角C的大小为（ ）
| 3 |
| A+B |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
将y=cos（
+
）的图象向右平移
个单位，所得曲线对应的函数（ ）
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、在（0，
| ||
B、在（0，
| ||
C、在（
| ||
D、在（
|
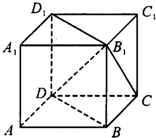如图，在正方体ABCD-A1B1C1D1中，