题目内容
若f（x）=ax3+bx2+cx+d（a＞0），则函数f（x）在R上为增函数的充要条件为（ ）
| A、b2＜3ac |
| B、b2＞3ac |
| C、b2≤3ac |
| D、b2≥3ac |
考点：函数的单调性与导数的关系
专题：导数的概念及应用
分析：先求出f′（x）=3ax2+2bx+c（a＞0），函数f（x）在R上为增函数，判别式小于等于0，问题得以解决．
解答：
解：∵f（x）=ax3+bx2+cx+d（a＞0），
∴f′（x）=3ax2+2bx+c（a＞0），
∵函数f（x）在R上为增函数
∴（2b）2-4×3ac≤0
即b2≤3ac
故选：C．
∴f′（x）=3ax2+2bx+c（a＞0），
∵函数f（x）在R上为增函数
∴（2b）2-4×3ac≤0
即b2≤3ac
故选：C．
点评：本题主要考查导数和函数的单调性，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项和为Sn，且a1=1，a2=3，若对任意n∈N*，都有an+2-an=2成立，则S100=（ ）
| A、2550 | B、2600 |
| C、5050 | D、5100 |
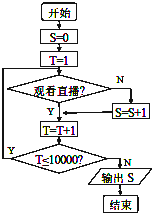为了解“伦敦奥运会开幕式”电视直播节目的收视情况，某机构在某地随机抽查了10000人，把抽查结果输入如图所示的程序框图中，其输出的数值是3700，则该节目的收视率为（ ）| A、3700 | B、630 |
| C、0.63 | D、0.37 |
已知向量
=（4cos（
x+
），sinx），
=（sin（
x+
），sinx），定义函数f（x）=
•
+cos2x．若f（α）=2，且14≤α≤18，则tan（απ）的值为（ ）
| a |
| π |
| 16 |
| π |
| 8 |
| b |
| π |
| 16 |
| π |
| 8 |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
由a1=1，d=3确定的等差数列{an}，当an=295时，序号n等于（ ）
| A、98 | B、99 | C、95 | D、100 |
定积分
cosxdx=（ ）
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
若关于x的不等式（x2-1）•（x-a）＜0没有正整数解，则实数a的最大值为（ ）
| A、3 | B、2 | C、1 | D、0 |