题目内容
将y=cos(
+
)的图象向右平移
个单位,所得曲线对应的函数( )
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、在(0,
| ||
B、在(0,
| ||
C、在(
| ||
D、在(
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件利用函数y=Acos(ωx+φ)的图象变换规律,余弦函数的图象的单调性,可得结论.
解答:
解:将y=cos(
+
)的图象向右平移
个单位,所得曲线对应的函数为y=cos(
+
)
=cos(
-
),
令2kπ≤
-
≤2kπ+π,k∈z,求得 4kπ+
≤x≤4kπ+
,
故所得函数的减区间为[4kπ+
,4kπ+
],k∈z,
结合所给的选项,
故选:C.
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
x-
| ||
| 2 |
| π |
| 6 |
=cos(
| x |
| 2 |
| π |
| 12 |
令2kπ≤
| x |
| 2 |
| π |
| 12 |
| π |
| 6 |
| 13π |
| 6 |
故所得函数的减区间为[4kπ+
| π |
| 6 |
| 13π |
| 6 |
结合所给的选项,
故选:C.
点评:本题主要考查函数y=Acos(ωx+φ)的图象变换规律,余弦函数的图象的单调性,属于基础题.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,且a1=1,a2=3,若对任意n∈N*,都有an+2-an=2成立,则S100=( )
| A、2550 | B、2600 |
| C、5050 | D、5100 |
定积分
cosxdx=( )
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
曲线y=x3+x2+x+1在点(-1,0)处的切线与抛物线y=ax2(a≠0)相切,则抛物线的准线方程是( )
A、y=-
| ||
B、y=
| ||
C、x=-
| ||
D、x=
|
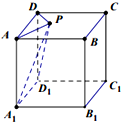 如图,正方体ABCD-A1B1C1D1中,P为面ABCD上一动点,且tan∠PA1A=2tan∠PD1D,则点P的轨迹是( )
如图,正方体ABCD-A1B1C1D1中,P为面ABCD上一动点,且tan∠PA1A=2tan∠PD1D,则点P的轨迹是( )| A、椭圆的一段 |
| B、双曲线的一段 |
| C、抛物线的一段 |
| D、圆的一段 |
若关于x的不等式(x2-1)•(x-a)<0没有正整数解,则实数a的最大值为( )
| A、3 | B、2 | C、1 | D、0 |
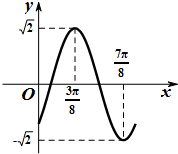 已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<