题目内容
已知函数f（x）=x3-x在（0，a]上单调递减，在[a，+∞）上单调递增，求a的值．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，根据函数的单调性建立不等关系即可得到结论．
解答：
解：∵f（x）=x3-x，
∴f′（x）=3x2-1，
∵函数f（x）=x3-x在（0，a]上单调递减，在[a，+∞）上单调递增，
∴当x=a时，函数f（x）取得极小值，
由f′（x）=3x2-1＞0，解得x＞
或x＜-
，此时函数单调递增，
由f′（x）=3x2-1＜0，解得-
＜x＜
，此时函数单调递减，
即x=
时，函数f（x）取得极小值，
即a=
．
∴f′（x）=3x2-1，
∵函数f（x）=x3-x在（0，a]上单调递减，在[a，+∞）上单调递增，
∴当x=a时，函数f（x）取得极小值，
由f′（x）=3x2-1＞0，解得x＞
| ||
| 3 |
| ||
| 3 |
由f′（x）=3x2-1＜0，解得-
| ||
| 3 |
| ||
| 3 |
即x=
| ||
| 3 |
即a=
| ||
| 3 |
点评：本题主要考查函数单调性和导数之间的关系，考查导数的应用，根据条件求出对应的极值是解决本题的关键．
练习册系列答案
相关题目
若关于x的不等式（x2-1）•（x-a）＜0没有正整数解，则实数a的最大值为（ ）
| A、3 | B、2 | C、1 | D、0 |
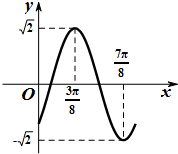已知函数f（x）=asin（ωx+θ）的部分图象如下图，其中ω＞0，|θ|＜
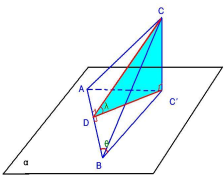如图，已知△ABC在平面α内的射影为△ABC′，若∠ABC′=θ，BC′=a，且平面ABC与平面α所成的角为λ，求点C到平面α的距离．