题目内容
7.设函数f(x)=(ax2+x-1)ex(a<0).(1)讨论f(x)的单调性;
(2)当a=-1时,函数y=f(x)与g(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2+m的图象有三个不同的交点,求实数m的范围.
分析 (1)求导f′(x)=(2ax+1)ex+(ax2+x-1)ex=ax(x+$\frac{2a+1}{a}$)ex,从而分类讨论以确定函数的单调性;
(2)当a=-1时,m=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2),再令h(x)=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2),从而求导可得.
解答 解:(1)∵f(x)=(ax2+x-1)ex,
∴f′(x)=(2ax+1)ex+(ax2+x-1)ex
=(ax2+(2a+1)x)ex
=ax(x+$\frac{2a+1}{a}$)ex,
当a=$-\frac{1}{2}$时,f′(x)≤0恒成立,
故函数f(x)在R上单调递减;
当a<$-\frac{1}{2}$时,
x<-$\frac{2a+1}{a}$时,f′(x)<0;-$\frac{2a+1}{a}$<x<0时,f′(x)>0;当x>0时,f′(x)<0;
故函数f(x)在(-∞,-$\frac{2a+1}{a}$)上单调递减,在(-$\frac{2a+1}{a}$,0)上单调递增,在(0,+∞)上单调递减;
当$-\frac{1}{2}$<a<0时,
x<0时,f′(x)<0;0<x<-$\frac{2a+1}{a}$时,f′(x)>0;当x>-$\frac{2a+1}{a}$时,f′(x)<0;
故函数f(x)在(-∞,0)上单调递减,在(0,-$\frac{2a+1}{a}$)上单调递增,在(-$\frac{2a+1}{a}$,+∞)上单调递减;
(2)当a=-1时,
f(x)-g(x)=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2+m),
故m=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2),
令h(x)=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2),
则h′(x)=-(x2+x)ex-(x2+x)=-x(x+1)(ex+1),
故当x<-1时,h′(x)<0;当-1<x<0时,h′(x)>0;当x>0时,h′(x)<0;
h(-1)=-$\frac{3}{e}$-$\frac{1}{6}$,h(0)=-1,
故-$\frac{3}{e}$-$\frac{1}{6}$<m<-1.
点评 本题考查了导数的综合应用及分类讨论的思想应用.

 学习实践园地系列答案
学习实践园地系列答案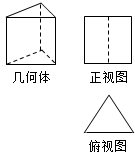 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )| A. | 8$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| y | 1.50 | 4.04 | 7.50 | 12.00 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).
| A. | $\frac{1}{4}$ | B. | $4\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | 64 |
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
| A. | 抛物线 | B. | 直线 | C. | 圆 |