题目内容
19．如果（m+4）${\;}^{-\frac{1}{2}}$＜（3-2m）${\;}^{-\frac{1}{2}}$，则m的取值范围是$（-\frac{1}{3}，\frac{3}{2}）$．分析 由（m+4）-${\;}^{\frac{1}{2}}$＜（3-2m）-${\;}^{\frac{1}{2}}$，可得m+4＞3-2m＞0，解出即可得出．
解答 解：∵（m+4）-${\;}^{\frac{1}{2}}$＜（3-2m）-${\;}^{\frac{1}{2}}$，
∴m+4＞3-2m＞0，
解得$-\frac{1}{3}＜m＜\frac{3}{2}$．
故m的取值范围为：$-\frac{1}{3}＜m＜\frac{3}{2}$．
故答案为：$（-\frac{1}{3}，\frac{3}{2}）$．
点评 本题考查了幂函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
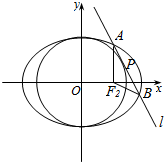已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{2}{3}$，F1、F2分别为其左、右焦点，点M为椭圆C的上的顶点，且，△MF1F2的面积为2$\sqrt{5}$．