题目内容
20.已知α是锐角,且cos(α+$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=$\frac{2\sqrt{2}}{3}$.分析 由已知利用诱导公式可求sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,结合角的范围,利用同角三角函数基本关系式计算可解.
解答 解:∵cos(α+$\frac{π}{6}$)=sin[$\frac{π}{2}$-(α+$\frac{π}{6}$)]=sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,
∵α是锐角,α-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{π}{6}$),
∴cos(α-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{3})}$=$\sqrt{1-(\frac{1}{3})^{2}}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
11.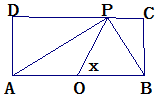 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )| A. | 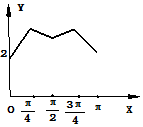 | B. | 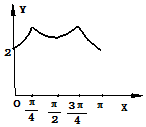 | ||
| C. | 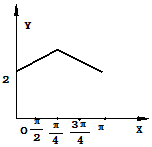 | D. | 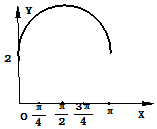 |
8.等比数列{an}的各项均为正数,且a5a6+a2a9=18,则log3a1+log3a2+…+log3a10的值为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
15.若复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,其中i为虚数单位,则a=( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
9.已知F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,椭圆C上存在点P使∠F1PF2为钝角,则椭圆C的离心率的取值范围是( )
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | (0,$\frac{1}{2}$) |
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.