题目内容
10.将函数$y=sin({x-\frac{π}{3}})$的图象上每点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到函数y=f(x)的图象.(1)求函数f(x)的解析式及其图象的对称轴方程;
(2)在△ABC中,内角A,B,C的对边分别为a,b,c.若$f(A)=\frac{{\sqrt{3}}}{2},a=2,b=\frac{{2\sqrt{3}}}{3}$,求sinB的值.
分析 (1)由题意和图象平移变换法则求出f(x)的解析式,由整体思想和正弦函数的对称轴方程求出其图象的对称轴方程;
(2)由(1)化简$f(A)=\frac{\sqrt{3}}{2}$,由内角的范围和特殊角的三角函数值求出A,由条件和正弦定理求出sinB的值.
解答 解:(1)由题意得,f(x)=$sin(2x-\frac{π}{3})$,
令$2x-\frac{π}{3}=\frac{π}{2}+kπ(k∈Z)$得,$x=\frac{5π}{12}+\frac{kπ}{2}(k∈Z)$,
所以f(x)的图象的对称轴方程是$x=\frac{5π}{12}+\frac{kπ}{2}(k∈Z)$;
(2)由(1)得,$f(A)=sin(2A-\frac{π}{3})=\frac{\sqrt{3}}{2}$,
因0<A<π,所以$-\frac{π}{3}<2A-\frac{π}{3}<\frac{4π}{3}$,
则$2A-\frac{π}{3}=\frac{π}{3}$或$2A-\frac{π}{3}$=$\frac{2π}{3}$,解得A=$\frac{π}{3}$或A=$\frac{π}{2}$,
当A=$\frac{π}{3}$时,因为$a=2,b=\frac{2\sqrt{3}}{3}$,
所以由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,
则$sinB=\frac{bsinA}{a}$=$\frac{\frac{2\sqrt{3}}{3}×\frac{\sqrt{3}}{2}}{2}$=$\frac{1}{2}$;
当A=$\frac{π}{2}$时,因为$a=2,b=\frac{2\sqrt{3}}{3}$,
所以由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,
则$sinB=\frac{bsinA}{a}$=$\frac{\frac{2\sqrt{3}}{3}×1}{2}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查正弦定理,三角函数图象平移变换法则,以及正弦函数的对称轴方程的应用,考查整体思想,化简、计算能力.

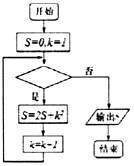
| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
| x | 0 | 1 | 3 | 4 |
| y | a | 4.3 | 4.8 | 6.7 |
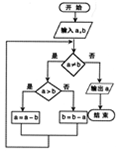 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )