题目内容
15.若复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,其中i为虚数单位,则a=( )| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
分析 由复数代数形式的乘除运算化简复数$\frac{a+i}{1+2i}$,又根据复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,列出方程组,求解即可得答案.
解答 解:$\frac{a+i}{1+2i}$=$\frac{(a+i)(1-2i)}{(1+2i)(1-2i)}=\frac{(2+a)+(1-2a)i}{5}$=$\frac{2+a}{5}+\frac{1-2a}{5}i$,
∵复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,
∴$\left\{\begin{array}{l}{\frac{2+a}{5}=0}\\{\frac{1-2a}{5}≠0}\end{array}\right.$,
解得:a=-2.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
6.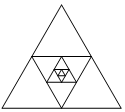 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |
3.设x,y满足约束条件$\left\{\begin{array}{l}x≥0,y≥0\\ x-y≥-1\\ x+y≤3\end{array}\right.$,则z=2x-y的最大值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | 6 |
5.如图所示的程序框图,若输出的结果为21,则判断框中应填入( )
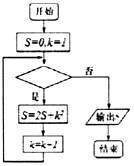

| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
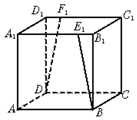 如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.
如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.