题目内容
11.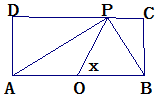 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )| A. | 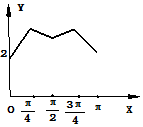 | B. | 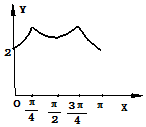 | ||
| C. | 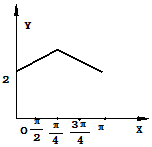 | D. | 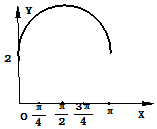 |
分析 根据函数图象关系,利用排除法进行求解即可.
解答 解:当0≤x≤$\frac{π}{4}$时,BP=tanx,AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{4+ta{n}^{2}x}$,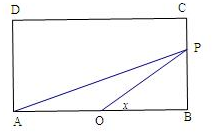
此时f(x)=$\sqrt{4+ta{n}^{2}x}$+tanx,0≤x≤$\frac{π}{4}$,此时单调递增,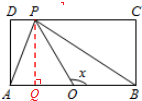
当P在CD边上运动时,$\frac{π}{4}$≤x≤$\frac{3π}{4}$且x≠$\frac{π}{2}$时,
如图所示,tan∠POB=tan(π-∠POQ)=tanx=-tan∠POQ=-$\frac{PQ}{OQ}$=-$\frac{1}{OQ}$,
∴OQ=-$\frac{1}{tanx}$,
∴PD=AO-OQ=1+$\frac{1}{tanx}$,PC=BO+OQ=1-$\frac{1}{tanx}$,
∴PA+PB=$\sqrt{(1-\frac{1}{tanx})^{2}+1}$+$\sqrt{(1+\frac{1}{tanx})^{2}+1}$,
当x=$\frac{π}{2}$时,PA+PB=2$\sqrt{2}$,
当P在AD边上运动时,$\frac{3π}{4}$≤x≤π,PA+PB=$\sqrt{4+ta{n}^{2}x}$-tanx,
由对称性可知函数f(x)关于x=$\frac{π}{2}$对称,
且f($\frac{π}{4}$)>f($\frac{π}{2}$),且轨迹为非线型,
排除A,C,D,
故选:B.
点评 本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤$\frac{π}{4}$时的解析式是解决本题的关键.

练习册系列答案
相关题目
1.已知函数f(x+1)=x2-x,则f(2)=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
6.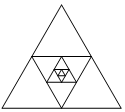 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |