题目内容
5.设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(0,$\frac{1}{2}$)的距离比点P到x轴的距离大$\frac{1}{2}$.(1)求点P的轨迹方程;
(2)若直线l:y=kx与点P的轨迹相交于A,B两点,且|AB|=2$\sqrt{6}$,求k的值.
(3)设点P的轨迹是曲线C,点Q(1,y0)是曲线C上的一点,求以Q为切点的曲线C的切线方程.
分析 (1)过P作x轴的垂线且垂足为N,由题意可丨PM丨-丨PN丨=$\frac{1}{2}$,.由y≥0,|PN|=y,知$\sqrt{{x}^{2}-(y-\frac{1}{2})^{2}}$=y-$\frac{1}{2}$,由此能求出点P的轨迹方程.
(2)设A(x1,y1),B(x2,y2),联立直线与抛物线方程,求得A和B点坐标,利用两点之间的距离公式即可求得k的值;
(3)由Q(1,y)是曲线C上一点,则x2=2y,y=$\frac{1}{2}$,求得切点坐标,由函数,求导得y'=x,由此能求出以Q为切点的曲线C 的切线方程.
解答 解:(1)过P作x轴的垂线且垂足为N,由题意可知:丨PM丨-丨PN丨=$\frac{1}{2}$,
而y≥0,∴|PN|=y,
∴$\sqrt{{x}^{2}-(y-\frac{1}{2})^{2}}$=y-$\frac{1}{2}$,
化简得x2=2y(y≥0)为所求的方程.…(4分)
(2)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}=2y}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=2k}\\{y=2{k}^{2}}\end{array}\right.$,
A(0,0),B(2k,2k2)
则丨AB丨=$\sqrt{4{k}^{2}+4{k}^{4}}$,
∴k4+k2-6=0而k2≥0,
∴k2=2,
∴k=±$\sqrt{2}$,
∴k的值±$\sqrt{2}$.…(8分)
(3)Q(1,y)是曲线C上一点,
∴x2=2y,y=$\frac{1}{2}$,
∴切点为(1,$\frac{1}{2}$),
由y=$\frac{1}{2}$x2,求导得y'=x,
∴当x=1时k=1,
则直线方程为y-$\frac{1}{2}$(x-1),
即2x-2y-1=0是所求切线方程.…(14分)
点评 本题考查轨迹方程的求法,考查直线与抛物线的为位置关系,两点之间的距离公式,利用导数求函数的单调性,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (0,1] | B. | (0,2] | C. | [1,2] | D. | [1,3] |
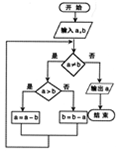 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )