题目内容
4.已知函数f(x)=$\frac{1}{e}•{e^x}+\frac{a}{2}{x^2}$-(a+1)x+a(a>0),其中e为自然对数的底数.若函数y=f(x)与y=f[f(x)]有相同的值域,则实数a的最大值为( )| A. | e | B. | 2 | C. | 1 | D. | $\frac{e}{2}$ |
分析 求出函数的导数,得到函数f(x)的值域,问题转化为即[1,+∞)⊆[$\frac{a}{2}$,+∞),得到关于a的不等式,求出a的最大值即可.
解答 解:f(x)=$\frac{1}{e}•{e^x}+\frac{a}{2}{x^2}$-(a+1)x+a(a>0),
f′(x)=$\frac{1}{e}$•ex+ax-(a+1),a>0,
则x<1时,f′(x)<0,f(x)递减,
x>1时,f′(x)>0,f(x)递增,
而x→+∞时,f(x)→+∞,f(1)=$\frac{a}{2}$,
即f(x)的值域是[$\frac{a}{2}$,+∞),恒大于0,
而f[f(x)]的值域是[$\frac{a}{2}$,+∞),
则要求f(x)的范围包含[1,+∞),
即[1,+∞)⊆[$\frac{a}{2}$,+∞),
故$\frac{a}{2}$≤1,解得:a≤2,
故a的最大值是2,
故选:B.
点评 本题考查了函数的单调性、值域问题,考查导数的应用以及转化思想,考查集合的包含关系,是一道中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.某校计划面向高一年级1200名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了180名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有105人.在这180名学生中选择社会科学类的男生、女生均为45人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
附:${K^2}=\frac{{n{{({ab-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.某几何体的三视图如图,则该几何体的体积是( )
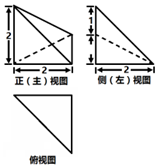

| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
13.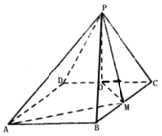 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.函数f(x)=$\frac{{sinx\sqrt{1-|x|}}}{{|{x+2}|-2}}$的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
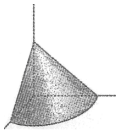 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).